MỤC LỤC BÀI VIẾT
Bài toán: Khảo sát hàm số $ \displaystyle y=\dfrac{{x+3}}{{x+1}}$
Giải:
Tập xác định: $D=\mathbb{R}\backslash \{-1\}$
Ta có: $ y\prime=\dfrac {-2}{(x+1)^2}<0 \forall x \in D \Rightarrow$ hàm số nghịch biến trên các khoảng $(-\infty;-1)$ và $(-1;+\infty)$
Giới hạn, tiệm cận:
$\lim\limits_{x\to +\infty } y=\lim\limits_{x\to -\infty } y=1\Rightarrow y=1$ là tiệm cận ngang của đồ thị hàm số.
$\lim\limits_{x\to-1^+} y=\lim\limits_{x\to -1^-} y=+\infty \Rightarrow x=-1$ là tiệm cận đứng của đồ thị hàm số.
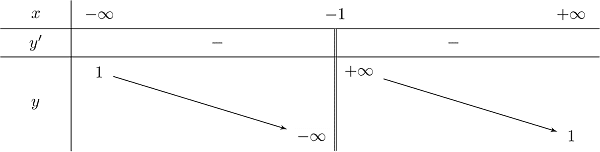
Bảng biến thiên: