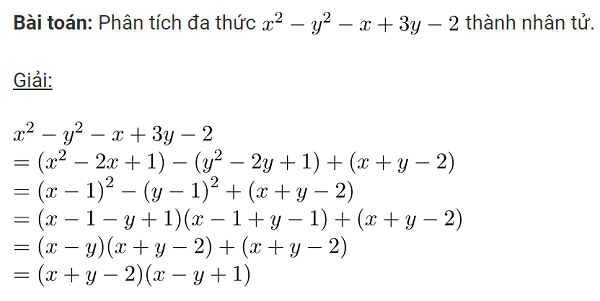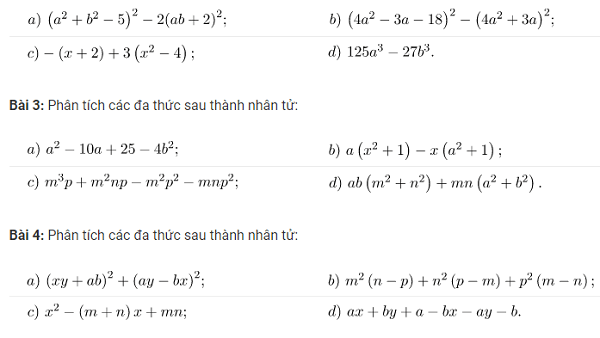Bài 1: Cho hai đa thức:

$ f( x )=2x^2-3x+x^3-4+6x-x^3-1;$

$ g( x )=3-2x^3+1-x+2x^3+x^2+3x $

a) Thu gọn và sắp xếp các đa thức trên theo lũy thừa giảm dần của biến;

b) Tìm đa thức h(x) sao cho h(x) = f(x) – g(x).

c) Tính h(2); h(-2).

Bài 2: Cho hai đa thức:

$Q( x )=x-5x^3-x^2-x^4+4x^3-x^2+3x-1 $

a) Thu gọn và sắp xếp các đa thức trên theo lũy thừa giảm của biến;

b) Tính P(x) + Q(x) và P(x) – Q(x).

Bài 3: Cho hai đa thức:

$P( x )=3x^5-5x^2+x^4-2x-x^5+3x^4-x^2+x+1;$

$Q( x )=-5+3x^5-2x+3x^2-x^5+2x-3x^3-3x^4 $

a) Thu gọn và sắp xếp các đa thức trên theo lũy thừa giảm dần của biến;

b) Tính P(x) + Q(x), P(x) – Q(x).

Bài 4: Cho đa thức $A( x )=4x^4+2x^3-x^4-x^2 $

a) Tìm hệ số cao nhất, hệ số tự do của đa thức;

b) Tính A(-1), A$\left( \dfrac {~1}{2} \right)$.

Bài 5: Cho hai đa thức:

$ f( x )=-x^5+2x^4-x^2-1;~g( x )=-6+2x-3x^3-x^4+3x^5$.

a) Tính h(x) = f(x) – g(x) ; q(x) = g(x) – f(x) tại x = -1, x = 1, x = -2, x =2;

b) Có nhận xét gì về hai đa thức h(x) và q(x) ?

Bài toán: Tìm giá trị lớn nhất (GTLN) của đa thức sau: $ A=6x-{{x}^{2}}-11$

Giải:

Hướng dẫn: Đưa về hằng đẳng thức thứ hai.

$ A=6x-{{x}^{2}}-11=-({{x}^{2}}-6x+9)-2$

$ \,A\,\,=-\left[ {{{{(x-3)}}^{2}}+2} \right]\le -2$ với mọi $ x$.

Giá trị lớn nhất của A là -2 ⇔ $ x-3=0\Leftrightarrow x=3$

Bài toán: Phân tích đa thức $ {{x}^{2}}-{{y}^{2}}-x+3y-2$ thành nhân tử.

Giải:

Hướng dẫn: Đưa về dạng hằng đẳng thức thứ ba.

$ \begin{array}{l}{{x}^{2}}-{{y}^{2}}-x+3y-2\\=({{x}^{2}}-2x+1)-({{y}^{2}}-2y+1)+(x+y-2)\\={{(x-1)}^{2}}-{{(y-1)}^{2}}+(x+y-2)\\=(x-1-y+1)(x-1+y-1)+(x+y-2)\\=(x-y)(x+y-2)+(x+y-2)\\=(x+y-2)(x-y+1)\end{array}$

Dưới đây là một số bài tập chia đa thức cho đa thức trong chương trình Đại số 8 – Toán lớp 8.

Bài 1: Thực hiện phép chia:

$ a)\left( {-3{{x}^{3}}+5{{x}^{2}}-9x+15} \right):\left( {-3x+5} \right);$	$ b)~\left( {5{{x}^{4}}+9{{x}^{3}}-2{{x}^{2}}-4x-8} \right):\left( {x-1} \right);$
$ c)~\left( {5{{x}^{3}}+14{{x}^{2}}+12x+8} \right):\left( {x+2} \right);$	$ d)~\left( {{{x}^{4}}-2{{x}^{3}}+2x-1} \right):\left( {{{x}^{2}}-1} \right).$

Bài 2: Làm phép chia bằng cách áp dụng hằng đẳng thức:

$ a)\left( {{{x}^{8}}-2{{x}^{4}}{{y}^{4}}+{{y}^{8}}} \right):\left( {{{x}^{2}}+{{y}^{2}}} \right);$	$ b)\left( {64{{x}^{3}}+27} \right):\left( {16{{x}^{2}}-12x+9} \right);$
$ c)\left( {{{x}^{3}}-9{{x}^{2}}+27x-27} \right):\left( {{{x}^{2}}-6x+9} \right);$	$ d)\left( {{{x}^{3}}{{y}^{6}}{{z}^{9}}-1} \right):\left( {x{{y}^{2}}{{z}^{3}}-1} \right).$

Bài 3:$ ~$Sắp xếp các đa thức sau theo lũy thừa giảm của biến rồi làm phép chia:

a) $ \left( {13x+41{{x}^{2}}+35{{x}^{3}}-14} \right):\left( {5x-2} \right);$

b) $ \left( {16{{x}^{2}}-22x+15-6{{x}^{3}}+{{x}^{4}}} \right):\left( {{{x}^{2}}-2x+3} \right);$

c) $ \left( {6x+2{{x}^{3}}-5-11{{x}^{2}}} \right):\left( {-x+2{{x}^{2}}+1} \right).$
Bài 4: Tìm m để đa thức $ 3{{x}^{3}}+2{{x}^{2}}-7x+m$ chia hết cho đa thức $ 3x-1$.

Bài 5: Tìm dư trong phép chia đa thức $ f\left( y \right)={{y}^{{243}}}+{{y}^{{81}}}+{{y}^{{27}}}+{{y}^{9}}+{{y}^{3}}+y$ cho đa thức $ g\left( y \right)={{y}^{2}}-1.$

Dưới đây là một số bài tập phân tích đa thức thành nhân tử cơ bản trong chương trình Đại số 8 – Toán lớp 8.

Bài 1: Phân tích các đa thức sau thành nhân tử:

$ a)~16{{x}^{2}}-8x+1-3\left( {4x-1} \right);$	$ b)~27{{x}^{3}}+8;$
$ c)-16{{x}^{4}}{{y}^{6}}-24{{x}^{5}}{{y}^{5}}-9{{x}^{6}}{{y}^{4}};$	$ d)~{{\left( {ax+by} \right)}^{2}}-{{\left( {ay+bx} \right)}^{2}}.$

Bài 2: Phân tích các đa thức sau thành nhân tử:

$ a)~{{\left( {{{a}^{2}}+{{b}^{2}}-5} \right)}^{2}}-2{{\left( {ab+2} \right)}^{2}};$	$ b)~{{\left( {4{{a}^{2}}-3a-18} \right)}^{2}}-{{\left( {4{{a}^{2}}+3a} \right)}^{2}};$
$ c)-\left( {x+2} \right)+3\left( {{{x}^{2}}-4} \right);$	$ d)~125{{a}^{3}}-27{{b}^{3}}.$

Bài 3: Phân tích các đa thức sau thành nhân tử:

$ a)~{{a}^{2}}-10a+25-4{{b}^{2}};$	$ b)~a\left( {{{x}^{2}}+1} \right)-x\left( {{{a}^{2}}+1} \right);$
$ c)~{{m}^{3}}p+{{m}^{2}}np-{{m}^{2}}{{p}^{2}}-mn{{p}^{2}};$	$ d)~ab\left( {{{m}^{2}}+{{n}^{2}}} \right)+mn\left( {{{a}^{2}}+{{b}^{2}}} \right).$

Bài 4: Phân tích các đa thức sau thành nhân tử:

$ a)~{{\left( {xy+ab} \right)}^{2}}+{{\left( {ay-bx} \right)}^{2}};$	$ b)~{{m}^{2}}\left( {n-p} \right)+{{n}^{2}}\left( {p-m} \right)+{{p}^{2}}\left( {m-n} \right);$
$ c)~{{x}^{2}}-\left( {m+n} \right)x+mn;$	$ d)~ax+by+a-bx-ay-b.$

Bài 5: Phân tích các đa thức sau thành nhân tử:

$ a)~3x-3y-{{x}^{2}}+2xy-{{y}^{2}};$	$ b)~{{x}^{2}}-4{{x}^{2}}{{y}^{2}}+{{y}^{2}}+2xy;$
$ c)~{{\left( {x+y} \right)}^{3}}-{{\left( {x-y} \right)}^{3}};$	$ d)~{{x}^{2}}-5x-14.$

Bài 6: Phân tích các đa thức sau thành nhân tử:

$ a)~{{m}^{6}}-{{m}^{4}}+2{{m}^{3}}+2{{m}^{2}};$	$ b)~{{a}^{3}}-3{{a}^{2}}+3a-1-{{b}^{3}};$
$ c)~2{{a}^{2}}\left( {x+y+z} \right)-4ab\left( {x+y+z} \right)+2{{b}^{2}}\left( {x+y+z} \right);$	$ d)~{{\left( {x+y} \right)}^{3}}-{{x}^{3}}-{{y}^{3}}.$

1. Tính giá trị:

B = x¹⁵ – 8x¹⁴ + 8x¹³ – 8x¹² + … – 8x² + 8x – 5 với x = 7

2. Cho ba số tự nhiên liên tiếp. Tích của hai số đầu nhỏ hơn tích của hai số sau là 50. Hỏi đã cho ba số nào?

3. Chứng minh rằng nếu: $ \displaystyle \frac{x}{a}=\frac{y}{b}=\frac{z}{c}$ thì

(x² + y² + z²) (a² + b² + c²) = (ax + by + cz)²