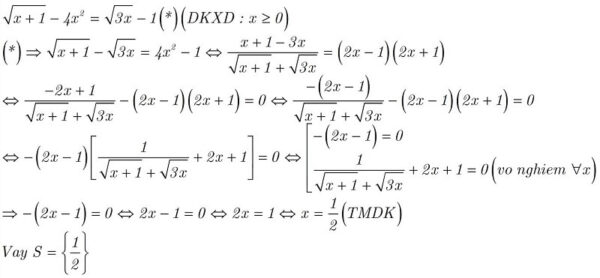Bài toán: Tìm nghiệm nguyên của phương trình x^2+y^2=xy+x+yGiải:Cách 1: Cách thông thường, áp dụng cho nhiều bài tìm nghiệm nguyên của phương trình.Ta có thể viết lại phương trình theo dạng:x^2 – x(y+1) + y^2 – y = 0Đây là một phương trình bậc hai đối với x, với hệ số a = 1, […]
Bài toán: Giải phương trình vô tỷ $ \displaystyle y^{2}-2y-y\sqrt{{2y+3}}+6=0$Giải:Điều kiện: $ \displaystyle {y\ge \dfrac{{-3}}{2}}$$ \displaystyle y^{2}-2y-y\sqrt{{2y+3}}+6=0$$ \displaystyle \Leftrightarrow 2y^{2}-4y-2y\sqrt{{2y+3}}+12=0$$ \displaystyle \Leftrightarrow \left( {y^{2}-6y+9} \right)+\left( {y^{2}-2y\sqrt{{2y+3}}+2y+3} \right)=0$$ \displaystyle \Leftrightarrow (y-3)^{2}+(y-\sqrt{{2y+3}})^{2}=0$$ \displaystyle \Leftrightarrow y=3$ (thỏa mãn)Vậy $y=3$ là nghiệm của phương trình đã cho.
Chúng ta có thể dùng phương pháp nhân liên hợp để giải một số phương trình chứa căn thức nâng cao với mục đích xuất hiện nhân tử chung.
Bài toán: Giải phương trình$x^{2}+\dfrac{9 x^{2}}{(x-3)^{2}}=16$Giải:Bằng cách thêm bớt rồi đặt ẩn phụ đưa phương trình đã cho về phương trình bậc 2 ẩn t. Sau đó giải t rồi tìm được $x$
Chúng ta có thể giải được phương trình bậc hai bằng cách biến đổi đưa về tìm giao điểm giữa đồ thị của 2 hàm số.
Bài tập phương trình bậc nhất, phương trình bậc hai đối với một hàm số lượng giác lớp 11 có lời giải kèm theo.
Dạng bài tập phương trình bậc nhất đối với sinX và cosX là dạng bài tập phương trình lượng giác cơ bản mà học sinh lớp 11 phải làm được.
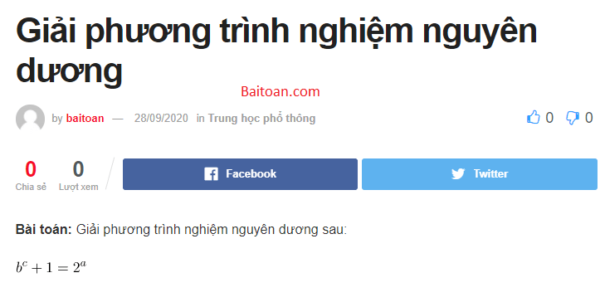
Bài toán: Giải phương trình nghiệm nguyên dương sau:$ \displaystyle {{b}^{c}}+1={{2}^{a}}$
Những bài toán giải phương trình vô tỉ (vô tỷ) ở lớp 9 thường có nhiều cách giải. Trong bài viết này Baitoan.com chia sẻ 2 cách thường dùng nhất.Các em theo dõi ví dụ dưới đây.Ví dụ: Giải phương trình sau$ \displaystyle {(4x-1)\sqrt{{{{x}^{2}}+1}}=2{{x}^{2}}+2x+1}$TXĐ = {R}Hướng giải:Với phương trình vô tỉ cơ bản thường giải […]