Từ khóa: toán nâng cao 5

Bài toán: Có ba tấm thẻ ghi số 1, một tấm thẻ ghi số 5, một tâm thẻ ghi số 7 và một tấm thẻ ghi số 8. Hỏi có thể lập được bao nhiêu số tự nhiên có sáu chữ số khi đặt sáu tấm thẻ này trên cùng một hàng?

Giải:

Số cách xếp các tấm thẻ là:

6x5x4x3x2x1=720 cách

Số lần lặp lại của chữ số 1 là:

3x2x1=6 lần

Số các số tự nhiên lập được là:

720 : 6 = 120 số

Bài toán: Một con hổ đuổi bắt một con thỏ ở cách nó 300m với vận tốc 60km/giờ. Con thỏ chạy trốn với vận tốc 42km/giờ cùng chiều với con hổ. Khi chạy được 6 giây, con thỏ phát hiện một con báo đang rình trước mặt để bắt nó, thỏ bèn quay ngược trở lại với vận tốc 36km/giờ.

a) Hỏi khi quay lại nó còn cách hổ bao nhiêu mét ?

b) Tính thời gian để hổ bắt được thỏ (tính từ khi thỏ quay ngược trở lại).

Giải:

a. 60 km/giờ = 50/3 m/giây; 42km/giờ = 35/3 m/giây; 36 km/giờ = 10 m/giây

Khoảng cách giữa thỏ và hổ khi thỏ quay lại là:

300 – (50/3 – 35/3) x 6 = 270 m

b.

Thời gian để hổ bắt được thỏ là:

270 : (50/3 + 10) = 10,125 giây.

Bài toán: Một con hổ đuổi bắt một con thỏ. Con hổ chạy với vận tốc 60 km/giờ, con thỏ chạy với vận tốc 55,8 km/giờ. Sau 5 phút rưỡi thì con hổ bắt được con thỏ. Hỏi trước khi đuổi bắt, con hổ cách con thỏ bao nhiêu mét ?

Giải:

60km/g=1000m/phút 55,8 km/g=930m/phút

Mỗi phút hổ chạy nhanh hơn thỏ 1000-930=70(m) 5,5 phút hổ chạnh nhanh hơn thỏ 70×5,5=385(m) Vậy trước khi đuổi bắt hổ cách thỏ 385m

Bài toán: Bạn An viết ra giấy một số thập phân. Sau đó An dịch dấu phẩy sang bên phải một chữ số rồi lấy số mới đó trừ đi số ban đầu thì được kết quả là 94,5. Hỏi số bạn An đã viết là số nào?

Giải:

Cách 1:

Gọi a,b là số thập phân

Ta có 10×a,b – a,b = 94,5

9×a,b = 94,5

Vậy a,b = 10,5

Cách 2:

Dịch dấu phẩy sang bên phải một chữ số mới kém số đó 10 lần. Vậy:

Số ban đầu (số lớn): 10 phần (bằng nhau) thì số mới (số bé) có 1 phần như thế.

Hiệu số phần bằng nhau là: 10-1-9 (phần).

Mỗi phần có giá trị số là: 94,5:9=10,5.

Số bé (số sau) là: 1×10,5=10,5

Số lớn (số ban đầu) là: 10×10,5=105

Bài toán: Hai người thợ cùng làm một công việc, nếu người thứ nhất làm một mình thì 6 ngày mới xong, người thứ 2 làm một mình thì 15 ngày mới xong. Đầu tiên một mình người thứ nhất làm trong một số ngày, sau đó người thứ 2 làm tiếp luôn thì tổng 9 ngày 2 người đã làm xong công việc. Hỏi mỗi người làm trong mấy ngày?

Giải:

Một ngày người thứ nhất làm một mình được số phần công việc là: 1: 6 = 1/6 (công việc)

Một ngày người thứ hai làm một mình được số phần công việc là: 1: 15 = 1/15 (công việc)

Giả sử người thứ nhất làm một mình cả 9 ngày thì số phần công việc làm được lúc này là: 1/6 x 9 = 3/2 (công việc)

Số phần công việc làm nhiều hơn so với thực tế là: 3/2 – 1 = 1/2 (công việc)

Mỗi ngày: người thứ nhất làm hơn người thứ hai số phần công việc là: 1/6 – 1/15 = 1/10 (công việc)

Số ngày người thứ hai làm một mình là: 1/2 : 1/10 = 5 (ngày)

Số ngày người thứ nhất làm một mình là: 9 – 5 = 4 (ngày)

Bài toán: Cho tam giác ABC có AM = NC = 1/4 AC; AI = IB; MI cắt CB tại Đ. Tính diện tích tứ giác DMNB, biết S.ABC = 168cm2.

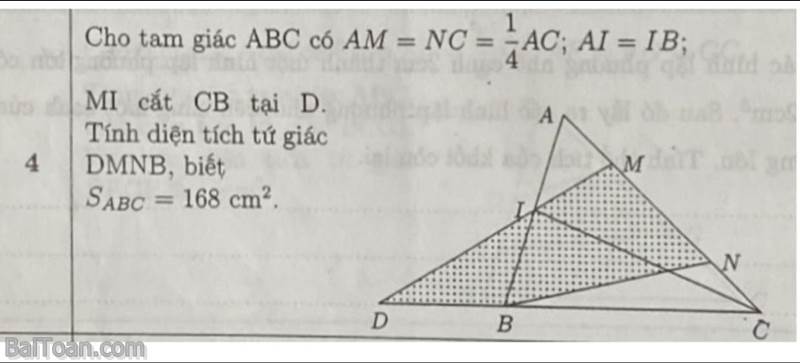
Giải:

Bài toán: Có 6 viên bi xanh, 8 viên bi trắng, 10 viên bi đỏ được trộn lẫn trong 1 chiếc hộp. Bạn Bình muốn lấy ra 2 viên bi của một màu này và 2 viên bi của một màu khác. Hỏi Bình phải lấy ít nhất bao nhiêu viên bi để chắc chắn có được điều đó?

Giải:

Trường hợp đen nhất là lấy được 10 viên đỏ, 1 viên xanh, 1 viên trắng thì chưa đủ 2 màu mỗi màu có 2 viên.

Bốc thêm phát nữa thì chắc chẵn sẽ có thêm 1 viên xanh hoặc 1 viên trắng, khi đó sẽ có 2 viên màu này và 2 viên màu kia.

Số bi bốc ra để chắc chắn có là:

10 + 1 + 1 + 1 = 13 viên

Bài toán: Cho hình tam giác ABC có diện tích là 60cm vuông. Trên AB lấy điểm N, sao cho BN = 1/4 AB. Trung điểm M nằm trên cạnh AC. Nối B với M và nối C với N. Hai đoạn thẳng BM và CN cắt nhau ở H. Tính diện tích hình tam giác HBC.

Giải:

Bổ sung sau dòng 5: Nối MN

Bài toán: Cho các chữ số: 0, 2, 4, 6. Có thể lập được bao nhiêu số thập phân có 4 chữ số khác nhau mà phần nguyên có 1 chữ số từ các chữ số đã cho?

Giải:

Phần nguyên có 4 cách chọn

Phần mười có 3 cách chọn (trừ 1 cách chọn phần nguyên)

Phần trăm có 2 cách chọn (trừ cách chọn phần mười)

Phần nghìn có 1 cách chọn (trừ cách chọn phần trăm)

Lập được các số khác nhau có 4 chữ số là

4×3×2×1=24 số

Bài toán: Cho tam giác ABC. Trên cạnh AB lấy điểm Q sao cho tỷ lệ QB/AB = 4/7, Trên cạnh AC lấy điểm K sao cho tỷ lệ AK/AC = 1/3. Biết diện tích tứ giác KQBC = 68cm vuông. Tính diện tích tam giác AKQ.

Giải:

Bài toán: Nếu tăng chiều dài của một hình chữ nhật thêm 25% và muốn diện tích hình chữ nhật không đổi thì chiều rộng phải tăng hay giảm bao nhiêu phần trăm?

Giải:

Chiều dài sau khi tăng bằng 125% chiều dài ban đầu.

Để diện tích không đổi (100% diện tích ban đầu) thì tỉ số % chiều rộng lúc sau so với lúc đầu là 100% ÷ 125% = 80%.

80% < 100% do đó chiều rộng hình chữ nhật lúc sau giảm: 100% – 80% = 20% so với chiều rộng ban đầu.

Bài toán: Cho tam giác ABC có AB = 9cm. Trên AC lấy điểm M sao cho MC bằng 1/2 AM. Trên BC lấy điểm N sao cho CN gấp đôi BN. Kéo dài AB và MN cắt nhau tại P. Tính độ dài BP.

Giải:

Bài toán: Một xe máy đi từ A với vận tốc 40 km/h về hướng C, sau một thời gian một ô tô cũng đi từ A với vận tốc 60 km/h về hướng C, hai xe dự định đến B cùng lúc. Cả 2 xe khi mỗi xe đã đi được 1/3AB thì thay đôi vận tốc, xe máy đi với vận tốc 50kmh, ô tô đi với vận tốc 62,5km/h nên hai xe đến C cùng lúc. Biết BC = 65km. Tính AC=…..?

Giải:

Gọi D là điểm có AD = 1/3 AB.

Tỷ số vận tốc giữa ô tô và xe máy là 60/40 = 3/2 nên với cùng thời gian đi thì quãng đường đi được của ô tô bằng 3/2 xe máy. Hay khi ô tô xuất phát thì xe máy đã đi được đến D.

Ô tô và xe máy đều tăng tốc quãng đường DC. Mỗi 1 km thì xe máy đi lâu hơn ô tô là:

1/50 – 1/62,5 = 1/250 (giờ)

Mỗi 1 km trên quãng đường AD thì ô tô đi hết thời gian là:

1 : 60 = 1/60 (giờ)

Thời gian ô tô đi trên quãng đường AD chính bằng thời gian xe máy đi lâu hơn ô tô trên quãng đường DC.

Ta có: DC/AD = 1/60 : 1/250 = 25/6

Coi AD là 6 phần thì DC là 25 phần nên BC là 13 phần.

Giá trị 1 phần là:

65 : 13 = 5 (km)

Quãng đường AC là: 5 x (25 +6) = 155 (km)

Bài toán: Người thợ thứ nhất sơn mỗi giờ được 15 cửa sổ, người thợ thứ hai sơn mỗi giờ được 20 cửa sổ. Người thợ thứ nhất làm trước 3 ngày. Hỏi từ khi Người thợ thứ hai đi làm thì sau bao nhiêu ngày lao động số cửa được sơn của hai người là như nhau ? Biết mỗi ngày làm việc 8 giờ.

Giải:

1 ngày người thứ nhất sơn được

15 x8 =120 cửa

1 ngày người thứ 2 sơn được

20 x8 =160 cửa

1 ngày người thứ 2 sơn nhiều hơn người thứ nhất

160 -120 =40 cửa

Số cửa người thứ nhất sơn trước

120 x3 =360 cửa

Số ngày 2 người sơn được số cửa bằng nhau kể từ khi người thưa 2 làm

360 :40=9 ngày

Bài toán 1: Từ A đi đến B một ôtô tải vận tốc 55 kmh,và một xe mô tô vận tốc 60 km/h xuất phát cùng lúc, Sau một thời gian một xe con xuất phát từ A đi được 1 giờ đuổi kịp xe tải, lúc này xe mô tô còn cách B 60 km, xe con và xe mô tô cùng đến B một lúc. Tính quãng đường AB?

Giải:

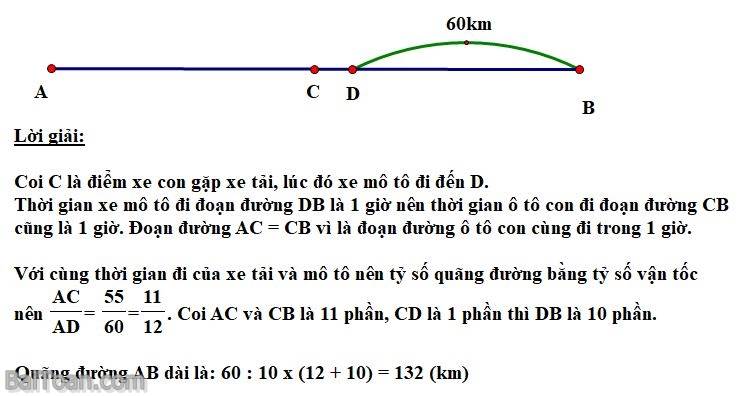
Bài toán 2: Một người đi từ A đến B với vận tốc 30 km/giờ dự định đến B lúc 11 giờ. Đi được 3/5 quãng đường AB thì người đó đi với vận tốc 40 km/giờ trên 1/2 quãng đường còn lại, rồi tiếp tục đi với vận tốc 45 km/giờ cho tới khi đến B, vậy nên người đó đếns B lúc 10 giờ 42 phút 30 giây. Tính quãng đường AB.

Giải:

Coi AC = 3/5 AB; CD = 1/5 AB

Trên quãng đường CD tỉ số vận tốc là 40/30 = 4/3 nên tỉ số tg là 3/4.

Tương tự trên DB tỉ số tg là 2/3.

Như vậy nếu coi tg đi trên 1/5 AB là 1 đơn vị thì tăng tốc giảm được số phần là:

2 – 3/4 – 2/3 = 7/12

7/12 đơn vị ứng với thời gian là:

11 giờ – 10 giờ 42 phút 30 giây = 17,5 (phút)

1 đơn vị tg ứng với số giờ là:

17,5 : 7 x 12 : 60 = 0,5 (giờ)

Quãng đường AB là:

30×0,5 x 5 = 75(km)

Bài toán 3: An và bình đi xe đạp cùng lúc từ A đến B, An đi với vận tốc 12 km/giờ, Bình đi với vận tốc 10km/giờ. Đi được 1,5 giờ, để đợi Bình, An đã giảm vận tốc xuống còn 7km/giờ. Tính quãng đường AB, biết rằng lúc gặp nhau cũng là lúc An và Bình cùng đến B?

Giải:

Khoảng cách giữa An và Bình sau 1,5 h là

(12-10)×1,5=3km

Thời gian An và Bình gặp nhau kể từ khi An giảm vận tốc là

3 :(10-7) =1h

Quãng đường AB dài

10 x (1, 5 +1)=25 km

Hoặc 12 x 1,5 +7×1=25 km

Bài toán: Trong hộp có 15 viên bi đỏ, 14 viên bi xanh, 10 viên bi vàng. Hỏi phải lấy ra ít nhất bao nhiêu viên bi thì chắc chắn rằng trong đó có 10 viên bi cùng màu?

Giải:

Trường hợp xấu nhất (đen nhất) trong số bi lấy ra có 9 bi đỏ, 9 bi xanh, 9 bi vàng, do đó cần bốc thêm 1 viên nữa để thỏa mãn yêu cầu.

Vậy số bi ít nhất cần lấy để có 10 viên cùng màu là:

9 x 3 + 1 = 28 viên

Bài 1: Một hộp có 3 loại bi màu đỏ, xanh, vàng tổng cộng là 120 viên. Số bi vàng chiếm 20% tổng số bi và bằng 80% bi đỏ. Tính số bi mỗi loại.

Bài 2: Nước biển chứa 5% muối. Hỏi phải thêm vào 200kg nước biển bao nhiêu kg muối để được dung dịch chứa 24% muối?

Giải:

Bài 1:

Số bi vàng là

120 x 20% = 24 viên

Số bi đỏ là

24 : 80% = 30 viên

Số bi xanh là

120 – (24 + 30) = 66

Bài 2:

Lượng nước có trong 200kg nước biển 5% muối là

200 x (100 – 5)% = 190kg

190kg chiếm số % trong nước 24% muối là

100 – 24 = 76%

Lượng muối cần thêm vào là

190 : 76% – 200 = 50kg

Bài toán: Khi nhân một số có 1 chữ số ở phần thập phân với 225, một bạn đặt các tích riêng thẳng cột với nhau như trong phép cộng vì vậy kết quả thu được giảm đi 27765. Tìm số thập phân trong phép nhân đó.

Giải:

Khi đặt tích riêng thẳng cột với nhau như trong phép cộng là bạn đó đã nhân số thập phân đó lần lượt với 5; 3; 2 rồi cộng kết quả lại với nhau.

Thừa số thứ hai giảm đi là:

235 – (5 + 3 + 2) = 225.

Số thập phân đó là:

27765 : 225 = 123,4

Bài 1: Tổ 1 lớp 5A có 11 em trồng được 44 cây, hỏi cả lớp nếu 48 em trồng được bao nhiêu cây, biết số cây mỗi em trồng được là như nhau.

Bài 2: Một tổ thợ mộc có 3 người trong 5 ngày đóng được 75 cái ghế. Hỏi nếu tổ đó có 5 người làm trong 7 ngày thì sẽ đóng được bao nhiêu cái ghế ? (biết năng suất mỗi người đều như nhau).

Bài 3: Một trường học huy động học sinh đi cuốc đất tăng gia, hôm đầu 30 em cuốc đất trong 2 giờ được 32m2. Hỏi hôm sau 50 em cuốc đất trong 3 giờ được bao nhiêu mét vuông ? (biết năng suất mỗi em đều như nhau)

Bài 4: 5 học sinh may 15 cái áo trong 3 giờ. Hỏi 8 học sinh may 32 cái áo mất bao lâu ? (biết năng suất mỗi người như nhau)

Bài 5: 8 người đóng xong 500 viên gạch trong 4 giờ. Hỏi 16 người đóng xong 1000 viên gạch mất bao lâu ? Biết năng suất mỗi người đều như nhau.

Bài 6: 9 người cuốc 540m2 đất xong trong 5 giờ. Hỏi 18 người cốc 270m2 đất xong trong bao lâu? (Biết năng suất mỗi người đều như nhau)

Bài 7: Một đơn vị bộ đội chuẩn bị đủ gạo cho 50 người ăn trong 10 ngày. 3 ngày sau được tăng thêm 20 người. Hỏi đơn vị cần chuẩn bị thêm bao nhiêu suất gạo nữa để đủ ăn trong những ngày sau đó (số gạo mỗi người ăn trong 1 ngày là một suất gạo)

Bài 8: Một đơn vị thanh niên xung phong chuẩn bị gạo đủ cho đơn vị ăn trong 30 ngày. Sau 10 ngày đơn vị nhận thêm 10 người nữa. Hỏi số gạo còn lại đó đơn vị sẽ đủ ăn trong bao nhiêu ngày? Biết lúc đầu đơn vị có 90 người.

Bài 9: 12 chị công nhân dệt trong 3 ngày được 120 tá áo. Hỏi nếu muốn dệt 180 tá áo trong 2 ngày cần bao nhiêu công nhân. Biết năng suất mỗi người như nhau.

Bài 10: Một cửa hàng có một số lít nước mắm đựng đầy trong các thùng, mỗi thùng chứa được 20 lít. Nếu đổ đủ số nước mắm đó vào các can, mỗi can chứa 5 lít, thì số can 5 lít phải nhiều hơn số thùng 20 lít là 30 cái. Hỏi cửa hàng có tất cả bao nhiêu lít nước mắm?

Bài 11: An và Bình cùng đọc một quyển truyện giống nhau. Trung bình mỗi ngày An đọc được 10 trang, Bình đọc được 15 trang. Hỏi quyển truyện dày bao nhiêu trang, biết An bắt đầu đọc sau Bình 2 ngày và Bình đọc xong trước An 7 ngày

Bài 12: Hai vòi nước cùng chảy vào một bể (không có nước) sau 6 giờ sẽ đầy bể. Hỏi nếu vòi một chảy một mình thì sau 10 giờ mới đầy bể. Hỏi nếu vòi hai chảy riêng một mình thì sau bao lâu sẽ đầy bể?

Bài 13: Một người đi từ tỉnh A đến tỉnh B bằng xe đạp, mỗi giờ đi được 12km. Từ B về A người đó đi bằng ô tô, mỗi giờ đi được 48km. Cả đi lẫn về mất 10 giờ. Hỏi quãng đường từ tỉnh A đến tỉnh B dài bao nhiêu ki – lô – mét?

Bài 14: Một cửa hàng có 28 thùng đựng đầy dầu gồm hai loại, loại thùng 60 lít và loại thùng 20 lít. Hỏi có bao nhiêu thùng mỗi loại, biết số dầu ở mỗi loại thùng đều bằng nhau.

Bài toán: Biết diện tích tam giác MNO = 28 cm2, RO = 3RN; RQ = MQ. Tính tổng diện tích phần tô màu.

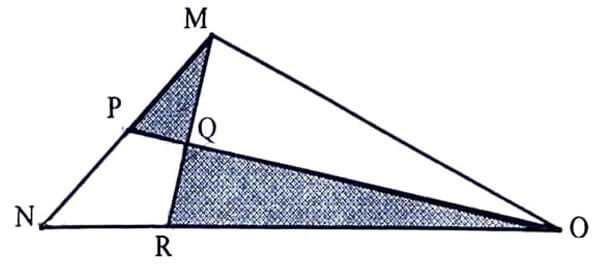
Giải:

S.MQO=S.RQO( đáy bằng nhau chung chiều cao hạ từ O).

S.PQM=S.PQR (đáy bằng nhau chung chiều cao hạ từ P)

S.PNR=1/3S.PRO (chung chiều cao hạ từ P đáy NR=1/3RO)

Mà S.PRO=S.POM=>S.PRN=28:(1+3+3)=4cm²

S tô đậm = (28-4):2=12cm2

Bài toán: Hàng ngày mẹ lái xe tới trường đón con rồi trở về nhà đúng thời gian. Hôm nay mẹ xuất phát từ nhà muộn 10 phút nhưng con lại được tan học sớm 30 phút nên tự đi về nhà trước với tốc độ 4,2 km/h, do đó mẹ đón được con và về sớm 2 phút so với mọi ngày. Coi tốc độ của xe trong suốt quá trình là không đổi.

a. Tính thời gian con đi bộ.

b. Xác định vận tốc lái xe của mẹ.

Giải:

Mẹ đi muộn 10 phút nhưng về sớm 2 phút nên thời gian đi giảm được 12 phút. Mỗi lượt đón con giảm được 6 phút.

Mẹ đi muộn 10 phút nhưng giảm được 6 phút nên khi đón con chỉ muộn 4 phút so với thời điểm đón con ở trường.

Thời gian con đi bộ là:

30 + 4 = 34 (phút)

Quãng đường con đi bộ 34 phút đã giúp mẹ giảm được 6 phút đi xe máy. Vận tốc xe máy của mẹ là:

4,2 x 34/6 = 23,8 (km/giờ).

Bài toán: Các số được lập từ các số nguyên từ 9 đến 88. Có ít nhất bao nhiêu số được rút ngẫu nhiên để chắc chắn có hai số mà tích của chúng chia hết cho 15?

Giải:

Số các số từ 9 đến 88 là:

88-9+1=80 số

Số các số chia hết cho 3 là:

(87 – 9) : 3 + 1 = 27 số

Số các số chi hết cho 5 là:

(85 – 10) : 5 + 1 = 16 số

Số các số chia hết cho 15 là:

(75 – 15) : 15 + 1 = 5 số

Số các không chia hết cho 3 hoặc 5 là:

80 – 27 – 16 + 5 = 42 số.

Trường hợp bốc cả 42 số không chia hết cho 3 hoặc 5 thì không có tích nào chia hết cho 15.

Bốc tiếp các số chia hết cho 3 mà không chia hết cho 5 (27 – 5 = 22 số) thì cũng không có tích của hai số nào chia hết cho 15.

Bốc thêm 1 số nữa thì số đó sẽ là số chia hết cho 5 nên chắc chắc trong các số bốc ra có 2 số có tích chia hết cho 15.

Trường hợp xấu nhất thì cần bốc là:

42 + 22 + 1 = 65 số.

Bài toán: Khi viết các số tự nhiên từ 1 đến 100 phải viết bao nhiêu chữ số 1, bao nhiêu chữ số 2?

Giải:

Xét các số 0; 1; 2;…;99.

Từ 00 đến 99 có 100 số có 2 chữ số có 2 chữ số

Số chữ số từ 0 đến 99 là:

2 x 100 = 200 chữ số

Các chữ số từ 0 đến 9 (10 chữ số) xuất hiện số lần như nhau.

Mỗi chữ số xuất hiện số lần là:

200 : 10 = 20 lần

Vậy có 20 chữ số 2 từ 1 đến 100

Số 100 có thêm 1 chữ số 1 nữa nên có 21 chữ số 1.

Bài toán: Một người bỏ ra 150 000 đồng tiền vốn để mua rau về bán. Sau khi bán hết người đó thu được 165 000 đồng. Hỏi:

a) Tiền bán bằng bao nhiêu tiền vốn?

b) Nếu lãi 25% tiền bán thì tiền lãi thu được là bao nhiêu?

Giải:

a)

Tỉ số % tiền bán và tiền vốn là:

165.000 : 150.000 x 100% = 110%

b)

Tỉ số % tiền vốn và tiền bán nếu lãi 25% tiền bán là:

100% – 25% = 75%

Tiền bán nếu lãi 25% tiền bán là:

150.000 : 75 x 100 = 200.000 đồng

Tiền lãi thu được là:

200.000 – 150.000 = 50.000 đồng

Bài toán: Một khách du lịch đi trên ô tô 4 giờ, sau đó đi tiếp bằng tàu hỏa trong 7 giờ được quãng đường dài 640km. Hỏi vận tốc của tàu hỏa và ô tô, biết rằng mỗi giờ tàu hỏa đi nhanh hơn ôtô 5km?

Giải:

Giả sử đi bằng ô tô cả 11 giờ được:

640 – 5×7= 605 km

Vận tốc ô tô là:

605:11 = 55 (km/giờ)

Vận tốc tàu hỏa là:

55+5=60 (km/giờ)

Bài toán: Số cam ở rổ thứ nhất bằng 3/7 số cam ở rổ thứ hai. Sau khi chuyển 3 quả từ rổ thứ hai sang rổ thứ nhất thì lúc này số cam ở rổ thứ nhất bằng 3/5 số cam ở rổ thứ hai. Tính số cam ở mỗi rổ lúc đầu?

Giải:

Ban đầu số cam ở rổ thứ nhất bằng 3/7 rổ thứ hai nên rổ thứ hai lúc đầu bằng 7/3 rổ thứ nhất hay bằng 7/10 tổng số cam

Lúc sau rổ thứ nhất bằng 3/5 rổ thứ hai hay nên rổ thứ hai bằng 5/3 rổ thứ nhất hay bằng 5/8 tổng số cam

Như vậy 3 quả cảm ứng với

7/10 – 5/8 = 3/40 tổng số cam

Vậy tổng số cam lúc đầu là

3 : 3/40 = 40 quả

Sau khi chuyển rổ thứ hai có số quả cam là:

40 x 5/8 = 25 quả

Lúc đầu rổ thứ hai có số quả cam là:

25 + 3 = 28 quả

Lúc đầu rổ thứ nhất có số quả cam là:

40 – 28 = 12 quả

Bài toán: Ba giá sách của một thư viện có tất cả 715 cuốn sách. Sau khi di chuyển đi 1/5 số sách ở giá thứ I, 1/6 số sách ở giá thứ II và 1/9 số sách ở giá thứ III thì số sách còn lại ở ba giá sách bằng nhau. Hỏi lúc đầu mỗi giá sách có bao nhiêu cuốn sách?

Giải

Phân số chỉ số sách còn lại mỗi ngăn bằng nhau nên 4/5 (I)=5/6(II)=8/9(III) hay 40/50(I)=40/48(II)=40/45(III)

Do đó coi số sách ngăn I là 50 phần, ngăn II 48 phần thì sách ở ngăn III sẽ là 45 phần

Như thế mỗi phần có số sách là 715:(50+48+45)=5 cuốn

Số sách ngăn I lúc đầu là: 5 x 50 = 250 cuốn

Số sách ngăn II lúc đầu là: 5 x 48 = 240 cuốn

Số sách ngăn III lúc đầu là: 5 x 45 = 225 cuốn

Bài toán: Hiện nay tuổi mẹ gấp 3 lần tổng số tuổi của hai chị em. Bốn năm sau tuổi mẹ gấp 2 lần tổng số tuổi của hai chị em. Tính tuổi mẹ hiện nay?

Hướng dẫn giải:

Hiện nay 2 chị em 1 phần tuổi, mẹ 3 phần tuổi

4 năm nữa mẹ 3 phần tuổi + 4 tuổi

2 chị em 1 phần tuổi + 8 tuổi

Tuổi mẹ khi đó gấp đôi tuổi 2 chị em

⇒ 1 phần tuổi + 4 tuổi = 8×2 =16 tuổi

⇒ 1 phần tuổi = 16 – 4 = 12 tuổi

⇒ Hiện nay tuổi mẹ là 12×3=36 tuổi

Bài toán: Một trường thuê một số xe bus để chở học sinh. Nếu mỗi xe chở 30 bạn thì một xe chỉ có 15 bạn. Nếu mỗi xe chở 35 bạn thì thừa 1 xe. Hỏi trường có bao nhiêu bạn?

Giải:

Số bạn còn thiếu để đủ mỗi xe 30 bạn là:

30 – 15 = 15 bạn

Số bạn để đủ mỗi xe 35 bạn thì nhiều hơn số bạn để đủ mỗi xe 30 bạn là:

35 – 15 = 20 bạn

Một xe 35 bạn thì nhiều hơn 1 xe 30 bạn là:

35 – 30 = 5 bạn

Số xe là:

20: 5 = 4 xe

Trường đó có số bạn là:

30 x 4 – 15 = 105 bạn

Bài toán: Hiện nay tuổi anh cả bằng số tuổi của anh hai và em út. Khi tuổi anh hai bằng tuổi anh cả hiện nay thì tuổi anh cả gấp 4 lần tuổi em út và tổng số tuổi của 3 anh em là 102 tuổi. Tính tuổi anh hai hiện nay?

Hướng dẫn giải:

Coi tuổi em út hiện nay là 1 đoạn thẳng. Khi tuổi anh hai bằng tuổi anh cả tức mỗi người tăng 1 đoạn thẳng và em út tăng tuổi gấp đôi so với hiện nay.

Suy ra hiện nay anh cả gấp 4 x 2 – 1 = 7 lần em út, anh hai gấp 6 lần em út.

Vẽ sơ đồ khi tổng số tuổi 3 người là 102: em út 2 đoạn, anh hai 7 đoạn, anh cả 8 đoạn.

Giá trị 1 phần là:

102 : (7+8+2) = 6 (tuổi)

Tuổi anh hai hiện nay là:

6 x (7-1) = 36 (tuổi)

Bài toán: Mẹ nuôi 20 con vừa vừa gà vừa chó. Hỏi có bao nhiêu con mỗi loại, biết số chân chó nhiều hơn số chân gà là 8 chân.

Giải:

Nếu thêm 4 con gà thì số chân gà tăng thêm 8 chân lúc đó số gà và chó là 20+4= 24 con và số chân gà bằng số chân chó .

Mà 1 chó có 4 chân gà có 2 chân vậy số gà gấp 2 số chó

Số chó là 24:(1+2)=8 con.

Số con gà là 20-8 =12 con

Bài toán: Một người bán một tấm vải được lãi 1/5 giá mua. Nếu người đó bán cao hơn 40 000 nữa thì được lãi 1/5 giá bán. Hỏi giá mua tấm vải?

Giải:

Lãi 1/5 giá bán tức là lãi bằng 1/4 giá mua.

Vậy 40 000 đồng tương ứng với:

1/4 – 1/5 = 1/20 (giá mua)

Giá mua tấm vải là:

40000:1/20 = 800000(đồng)

Bài toán: Một bà mẹ có 1 con gái và 1 con trai. Năm nay mẹ 32 tuổi, con gái 6 tuổi và con trai 2 tuổi. Hỏi sau bao nhiêu năm nữa thì số tuổi của mẹ gấp rưỡi tổng số tuổi của hai con?

Giải:

Gấp rưỡi = 3/2. Giả sử tuổi bố bằng tuổi mẹ.

Tổng tuổi hai con hiện nay là:

6 + 2= 8 tuổi.

Tổng tuổi bố và mẹ hiện nay là:

32 + 32 = 64

Tổng tuổi bố và mẹ hơn tổng tuổi hai con là:

64 – 8 = 56 tuổi

Khi tuổi mẹ gấp rưỡi tổng tuổi hai con thì tổng tuổi bố và mẹ gấp tuổi hai con số lần là:

3/2 x 2 = 3 lần

Khi tổng tuổi bố và mẹ gấp 3 lần tổng tuổi hai con thì tổng tuổi hai con là:

56 : (3 – 1) = 28 tuổi.

Tuổi mẹ gấp rưỡi tổng tuổi hai con sau số năm là:

(28 – 8 ) : 2 = 10 năm

Đáp số: 10 năm

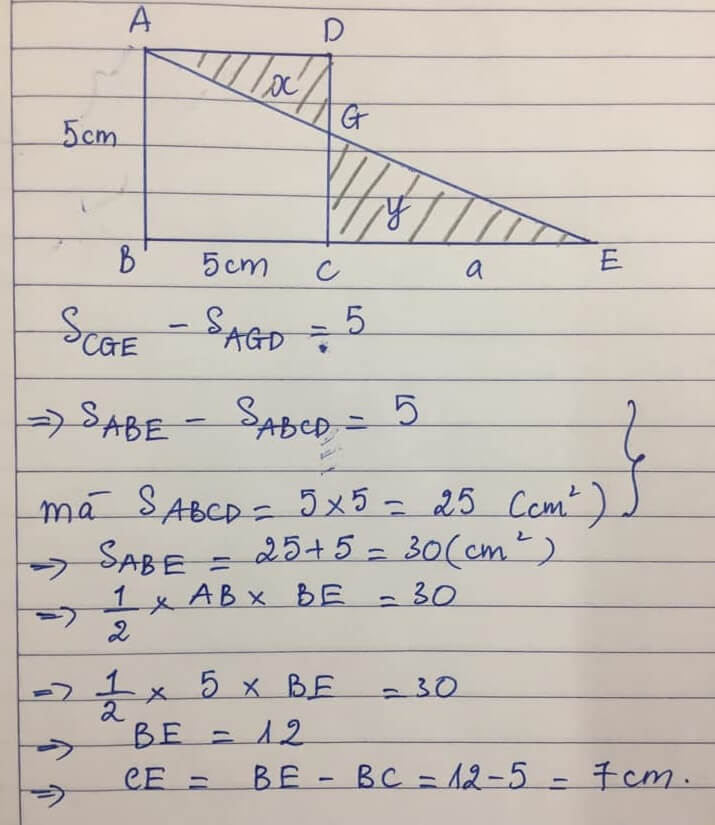
Bài toán: Cho hình vuông ABCD cạnh 5cm (hình vẽ). Kéo dài BC đến E, nối AE biết S_CGE – S_AGD = 5cm²

CE = …?cm.

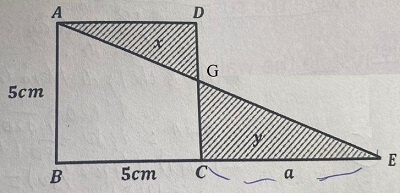
Giải:

Bài toán : Các tích sau đây có tận cùng bao nhiêu chữ số 0?

a) A = 20 x 21 x 22 x 23 x . . . x 28 x 29

b) B = 28 x 29 x 30 x 31 x . . . x 81 x 82

c) C = 5 x 77 x 25 x 32 x 8 x 125

Giải:

a) A = 20 x 21 x 22 x 23 x . . . x 28 x 29

Tích trên có 1 số tròn chục là 20 nên tích tận cùng bằng 1 chữ số 0

Ta lại có 25 = 5 x 5 nên 2 thữa số 5 này khi nhân với 2 só chẵn cho tích tận cùng bằng 2 chữ số 0

Vậy tích trên tận cùng bằng 3 chữ số 0.

b) B = 28 x 29 x 30 x 31 x . . . x 81 x 82

Gồm 6 số tròn chục là 30, 40, 50, 60, 70, 80 sẽ tạo được 6 chữ số 0               (1)

Các số có tận cùng  là 5: 35 = 7 x 5, 45 = 9 x 5, 55 = 11 x 5, 65 = 13 x 5, 75 = 15 x 5 = 3 x 5 x 5

Ngoài ra 50 = 10 x 5

→ Có tất cả 7 chữ số 5

5 nhân với số chẵn sẽ tạo ra chữ số tròn chục.

→ Tạo được 7 chữ số 0                (2)

Từ (1) và (2) suy ra tích trên có 6 + 7 = 13 chữ số 0.

c) C = 5 x 77 x 25 x 32 x 8 x 125

5 x 25 x 125=5 x (5 x 5) x (5 x 5 x 5)

8 x 32=(2 x 2 x 2) x (2 x 2 x 2 x 2 x 2)

Mà 5 nhân với số chẵn sẽ ra số tận cùng bằng 0

Theo cách phân tích trên sẽ có 6 cặp 5 x 2.

Vậy tích ban đầu sẽ có tận cùng là 6 chữ số 0

Bài toán: Hình dưới

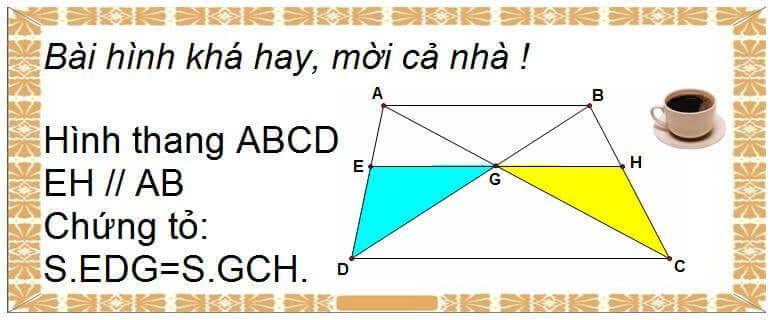
Đáp án

Lời giải của thầy Cao Hữu Hiền:

S.ADC = S.BDC

S.EDC = S.HDC

Trừ 2 biểu thức trên cho nhau ta có:

S.AEC = S.BDH

Mà S.AEC = h x EG : 2

S.BDH = h x GH : 2

Suy ra EG = GH nên Xanh = Vàng

(h là chiều cao hình thang)

Bài toán: Hồng và Nhung cùng gấp hoa. Hồng gấp được nhiều hơn Nhung 17 bông. Khi Nhung cho Hồng 2 bông thì số hoa của Nhung bằng 2/5 số hoa của Hồng. Hỏi lúc đầu mỗi bạn gấp được bao nhiêu bông hoa?

Giải:

Nếu Nhung đưa Hồng 2 bông thì lúc này Hồng hơn Nhung số hoa là: 17+2+2= 21 bông.

Số hoa của Nhung lúc này là 2 phần, của Hồng là 5 phần. Chênh lệch là:5-2= 3 phần ứng với 21 bông hoa.

Số hoa ban đầu của Nhung là: 21:(5-2)x2+2 = 16 bông

Số hoa ban đầu của Hồng là: 16+17= 33 bông.

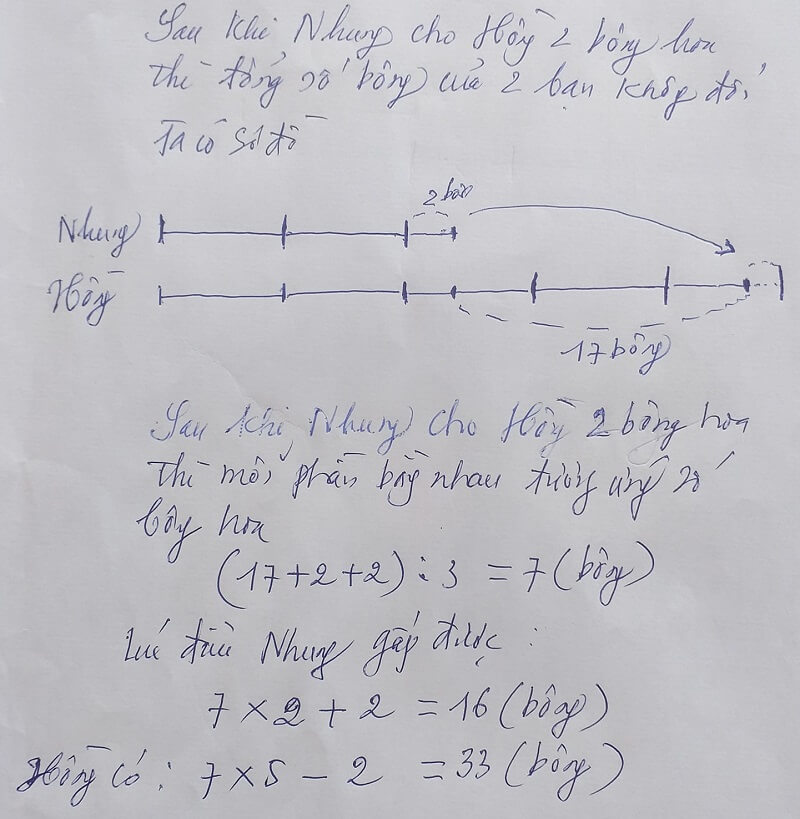
Bài toán: Mai chuyển 15 quyển sách từ ngăn 1 sang ngăn 2 thì thấy tỉ số sách ngăn 1 và ngăn 2 là 10/21, sau đó Mai lại chuyển 25 quyển sách từ ngăn 2 sang ngăn 1 thì thấy tỉ số sách ngăn 1 và ngăn 2 là 15/16. Tính tổng số sách hai ngăn.

Giải:

Sau khi chuyển đi chuyển lại thì tổng số sách hai ngăn không đổi.

Phân số chỉ số sách ngăn 1 trước khi nhận 25 quyển là:

10 : (10+21) = 10/31 (tổng số sách)

Phân số chỉ số sách ngăn 2 sau khi nhận 25 quyển là:

15 : (15+16) = 15/31 (tổng số sách)

Phân số chỉ 25 quyển sách ngăn 1 là:

15/31 – 10/31 = 5/31 (tổng số sách)

Tổng số sách hai ngăn là:

25 : 5/31 = 155 quyển

Bài toán: Lớp 5A có 1/4 số học sinh là học sinh trung bình, số học sinh giỏi bằng 2/3 số học sinh khá và không có học sinh yếu kém. Biết số học sinh giỏi hơn số học sinh trung bình 2 bạn. Tính số học sinh của lớp 5A.

Giải:

Số học sinh khá và giỏi (khá giỏi) bằng:

1 – 1/4 = 3/4 (số học sinh cả lớp)

Số học sinh giỏi = 2/3 số học sinh khá nên số học sinh giỏi bằng:

2 : (2 + 3) = 2/5 (số học sinh khá giỏi)

Và số học sinh giỏi bằng:

2/5×3/4 = 3/10 (số học sinh cả lớp)

Số học sinh giỏi hơn số học sinh trung bình là: 3/10 – 1/4=1/20 (số học sinh cả lớp) ứng với 2 học sinh

⇒ Số học sinh cả lớp là 2:1/20=40 (học sinh)

Bài toán: Một số tự nhiên khi chia cho 5 dư 2, chia cho 8 dư 5 và hiệu của hai thương là 423. Tìm số đó?

Giải:

Cách 1:

Thêm 3 thì chia hết cho cả 5 và 8, mỗi tương tăng thêm 1 đơn vị nên hiệu 2 thương vẫn là 423.

Tỉ số thương chia 8 và thương chia 5 là:

5 : 8 = 5/8

Thương chia 8 sau khi thêm là:

423 : (8-5)x5=705

Số đó sau khi thêm là:

705 x 8 = 5640

Số phải tìm là:

5640 – 3 = 5637

Cách 2:

Số nhỏ nhất chia 5 dư 2 & chia 8 dư 5 là 37.

Hiệu 2 thương là 3.

Số nhỏ nhất chia hết cho cả 5 & 8 là 40, hiệu 2 thương là 3

Số cần tìm là

(423 – 3 ) ÷ 3 × 40 + 37 = 5637

Bài toán: Lớp 5D có một số học sinh nam và nữ, trong đó 45% tổng số học sinh là nữ. Sau khi chuyển đi 3 bạn nữ và chuyển đến 13 bạn nam thì số bạn nữ là 30% tổng số học sinh cả lớp. Tính số học sinh nữ và số học sinh nam lớp 5D.

Lời giải

Ai giải được bài toán này comment ngay bên dưới nào.

Hướng dẫn giải các bài toán hình học nâng cao lớp 5 qua các bài tập có phân tích, hướng dẫn kèm lời giải dưới đây.

Bài toán: Ngăn thứ nhất có 550 quyển sách. Ngăn thứ hai có 450 quyển sách . Số sách Tiếng Việt ở hai ngăn bằng nhau và 3 lần số sách Toán ngăn thứ nhất bằng 5 lần số sách Toán ngăn thứ hai. Hỏi mỗi ngăn có bao nhiêu quyển sách Toán?

Giải:

Bài toán: Hiện nay tuổi bố gấp 10 lần tuổi con. Biết rằng 6 năm nữa tuổi bố gấp 4 lần tuổi con. Tính tuổi bố và tuổi con hiện nay?

Giải:

Hiện nay tuổi con là 1 phần, tuổi bố là 10 phần. Hiệu số tuổi của bố và con là 9 phần. Tuổi con bằng 1/9 hiệu số tuổi .

6 năm sau tuổi con bằng 1/4 tuổi bố. Hiệu số tuổi của bố và con là 3 phần. Tuổi con bằng 1/3 hiệu số tuổi của bố và con.

Hiệu số tuổi luôn không đổi.

Vậy 6 tuổi ứng với:

1/3 – 1/9 = 2/9 (hiệu số tuổi của bố và con)

Hiệu số tuổi của bố và con là: 6 : 2/9 = 27 (tuổi)

Tuổi con hiện nay là: 27 ×1/9= 3 (tuổi)

Tuổi bố hiện nay là: 3×10=30 (tuổi)

Bài toán: Một người có số gạo nếp bằng 2/3 số gạo tẻ. Sau khi người đó bán đi 35kg gạo tẻ thì số gạo nếp bằng 3/4 số gạo tẻ còn lại. Hỏi lúc đầu người đó có bao nhiêu kg gạo mỗi loại?

Giải:

Số gạo nếp là 6 phần thì số gạo tẻ lúc đầu là:

6 : 2/3= 9 phần

số gạo tẻ sau khi bán 35 kg là:

6 : 3/4= 8 phần

Vậy 35 kg gạo tẻ ứng với số phần là:

9 – 8=1 phần

Số gạo tẻ có lúc đầu

35 x 9 = 315 kg

Số gạo nếp có là

35 x 6 =210 kg

Bài toán 1: Cho hình thang ABCD. Nối A với C, nối B với D. AC và BD cắt nhau tại O. K là trung điểm của đáy lớn DC. Nối OK kéo dài cắt đáy nhỏ AB tại I. So sánh diện tích AIKD và BIKC.

Bài toán 2: Tam giác ABC có diện tích là 270m2. Trên AB lấy D,E sao cho AD = DE=EB. Trên AC lấy H, K sao cho AH=HK=KC. Trên BC lấy M, N sao cho BM=MN=NC. Tính diện tích hình DEMNKH.

Hướng dẫn giải:

Bài toán 1:

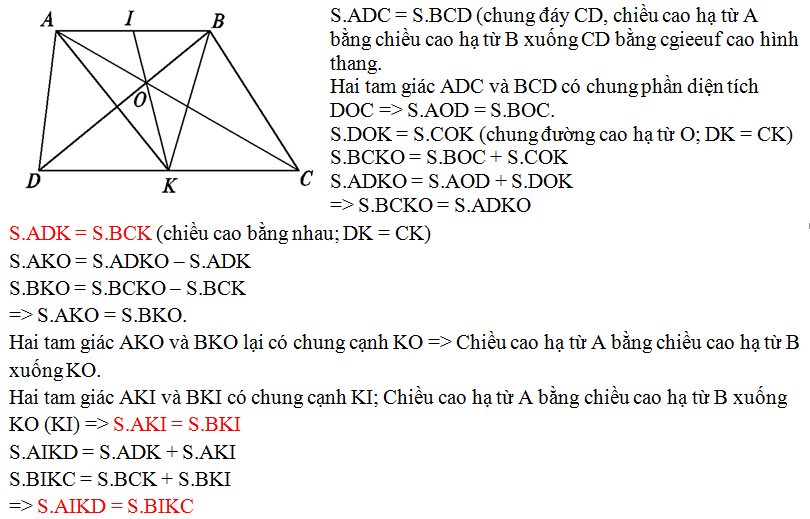
Bài toán: Cho một số tự nhiên gồm các số tự nhiên liên tiếp từ 1 đến 2020, được viết theo thứ tự liền nhau như sau:
1 2 3 4 5 6 7 8 9 10 11 12 13 … 2017 2018 2019 2020.

Hãy tính tổng tất cả các chữ số của số đó ?

Giải:

Bước 1: Tính tổng các chữ số từ 0 đến 999

Thêm các chữ số 0 vào để ta có dãy toàn các số có 3 chữ số: 000, 001,…, 999. Tổng các chữ số không thay đổi.

Dãy trên có 1000 số, có tổng số chữ số là: 3 x 1000 = 3000 (chữ số)

Mỗi chữ số 0,1,…,9 xuất hiện số lần là: 3000 : 10 = 300 (lần)

Do vậy tổng tất cả các chữ số từ 000 đến 999 là:

(0 + 1 + 2 +… + 9) x 300 = 45 x 300 = 13500

Bước 2: Tính tổng các chữ số từ 1000 đến 1999:

So với dãy số 000 đến 999 thì mỗi số tăng thêm 1 ở hàng nghìn. Do vậy tổng số chữ số là:

13500 + 1 x 1000 = 14500.

Bước 3: Tổng từ 2000 đến 2020: 2×21+10×1+2+2×45=144

Vậy tổng các chữ số từ 0 đến 2020 là:

13500 + 14500 + 144 = 28144

 

Bài toán: Sau 3 bài kiểm tra, một lớp có số bạn được 3 điểm 10 bằng số bạn được 1 điểm 10 và bằng 1/3 số bạn được 2 điểm 10. Tính số học sinh lớp đó biết tổng số điểm 10 là 60 và có 4 bạn chưa được điểm 10.

Giải:

Nhóm 1 bạn 3 điểm 10, 1 bạn 1 điểm 10 và 3 bạn 2 điểm 10 thành 1 nhóm
Số bạn trong nhóm là:
1+1+3=5 bạn
Số điểm 10 trong nhóm là:
3×1+1×1+2×3=10 điểm 10
Số nhóm là:
60:10= 6 nhóm
Số bạn được điểm 10 là:
5×6=30 bạn
Số học sinh lớp đó là:
30+4=34 bạn

Bài toán: Người thứ 1 đi từ A đến B hết 2 giờ, người thứ 2 đi từ B đến A hết 1 giờ 30 phút. Nếu hai người xuất phát cùng một thời điểm hỏi sau bao lâu họ gặp nhau trên đường.

Giải:

Bài toán: Viết các tổng sau thành tích của 2 thừa số:

a, 132 + 77 + 198

b, 5555 + 6767 + 7878

c, 1997, 1997 + 1998, 1998 + 1999, 1999

Giải

a, 132 + 77 + 198
= 11 x 12 + 11 x 7 + 11 x 18
= 11 x (12 + 7 + 18) ( nhân 1 số với 1 tổng)
= 11 x 37

b, 5555 + 6767 + 7878
= 55 x 101 + 67 x 101 + 78 x 101
= 55 + 67 + 78) x 101
= 200 x 101

c, 1997, 1997 + 1998, 1998 + 1999, 1999
= 1997 x 1,0001 + 1998 x 1,0001 + 1999 x 1,0001
= (1997 + 1998 + 1999) x 1,0001
= 5994 x 1,0001 ( nhân 1 tổng với 1 số)