Bài toán: Khảo sát hàm số $y=x^4-2x^2-3$ và $y=-x^4-2x^2-3$.
Giải:
Khảo sát hàm số $y=x^4-2x^2-3$
Tập xác định: $D=\mathbb{R}$
Chiều biến thiên:
Ta có: $ y\prime=4x^3-4x$
$ y\prime=0 \Leftrightarrow x=0$ hoặc $ x=\pm1$
$ y\prime>0 \Leftrightarrow x \in (-1;0) \cup (1;+\infty)$; $ y\prime<0 \Leftrightarrow (-\infty;-1) \cup (0;1)$
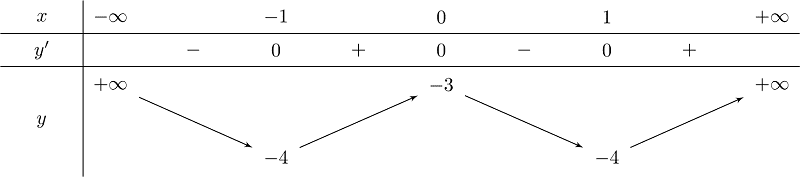
Hàm số nghịch biến trên các khoảng $(-\infty;-1) \cup (0;1)$, đồng biến trên các khoảng $(-1;0) \cup (1;+\infty)$
Hàm số đạt cực đại tại điểm $ x=0$, giá trị cực đại của hàm số là $ y(0)=-3$
Hàm số đạt cực tiểu tại điểm $ x=\pm1$, giá trị cực tiểu của hàm số là $ y(\pm1)=-4$
Giới hạn của hàm số tại vô cực: $\lim\limits_{x\to -\infty } =+\infty$; $\lim\limits_{x\to +\infty } =-\infty$
Bảng biến thiên:
Khảo sát hàm số $y=-x^4-2x^2-3$
Tập xác định: $D=\mathbb{R}$
Chiều biến thiên:
Ta có: $ y\prime=-4x^3-4x$
$ y\prime=0 \Leftrightarrow x=0$
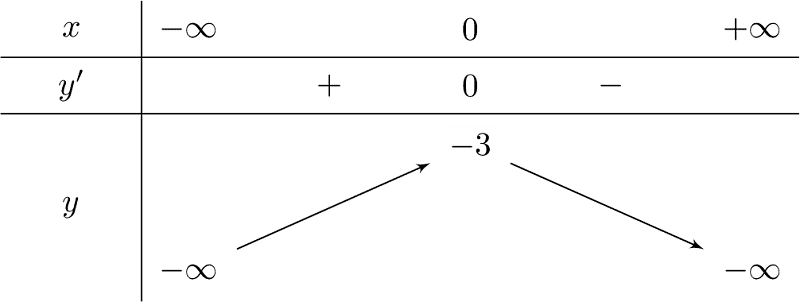
Hàm số đồng biến trên khoảng $(-\infty;0)$; nghịch biến trên khoảng $(0;+\infty)$
Hàm số đạt cực đại tại điểm $ x=0$, giá trị cực đại của hàm số là $ y(0)=-3$
Giới hạn của hàm số tại vô cực: $\lim\limits_{x\to -\infty } =-\infty$; $\lim\limits_{x\to +\infty } =-\infty$
Bảng biến thiên: