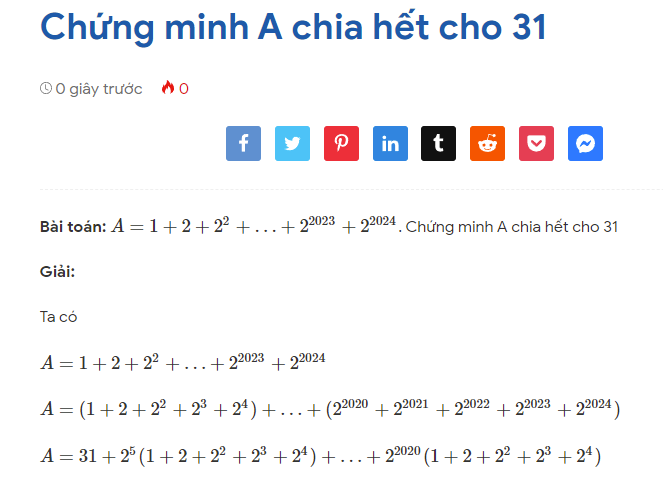
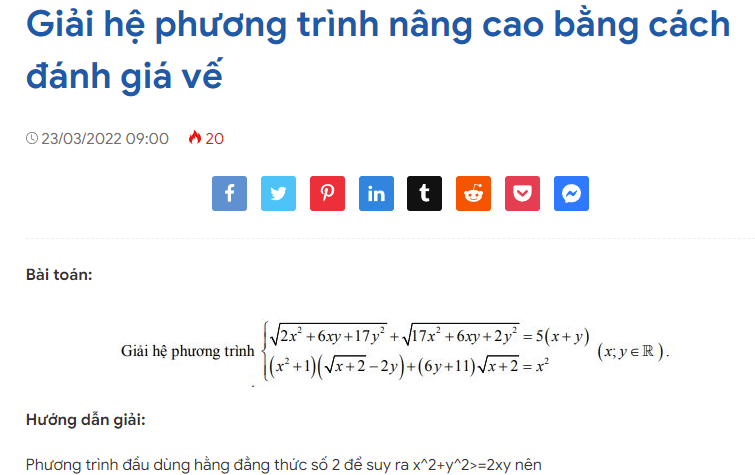
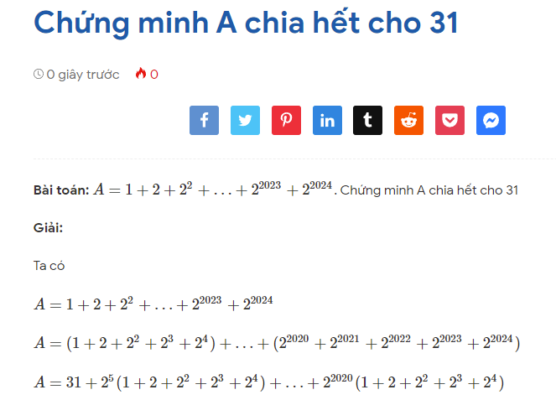
Bài toán: Một học sinh được giao thiết kế một cái hộp dạng hình hộp chữ nhật thỏa mãn: Tổng của chiều dài và chiều rộng bằng 12cm, tổng của chiều rộng và chiều cao là 24cm. Giáo viên yêu cầu học sinh ấy thiết kế sao cho thể tích cái hộp lớn nhất, giá trị lớn nhất ấy bằng bao nhiêu?
Hướng dẫn giải:
Gọi x là chiều rộng, chiều dài là 12-x, chiều cao là 24-x.
Thể tích cái hộp là V= x.(12-x)(24-x)
Chọn hệ số phụ m, n sao cho mx = n(12-x) = 24-x (Cô si tích ra tổng sao cho khử được x)
mnV=mx.(12n-nx)(24-x)
và mx-nx-x = 0
Từ đó m=n+1 hay (n+1)x = n(12-x) = 24-x từ đây tìm được m,n.
n=1+căn3 và m=2+căn3.
Khi đó: (1+căn3)(2+căn3).V= (mx).(12n-nx)(24-x)
Cô si tích thành tổng là khử được x.
V lớn nhất = 384.căn3
Khi Rộng = 12-4.căn3; Dài = 4.căn3; Cao = 12+4.căn3.