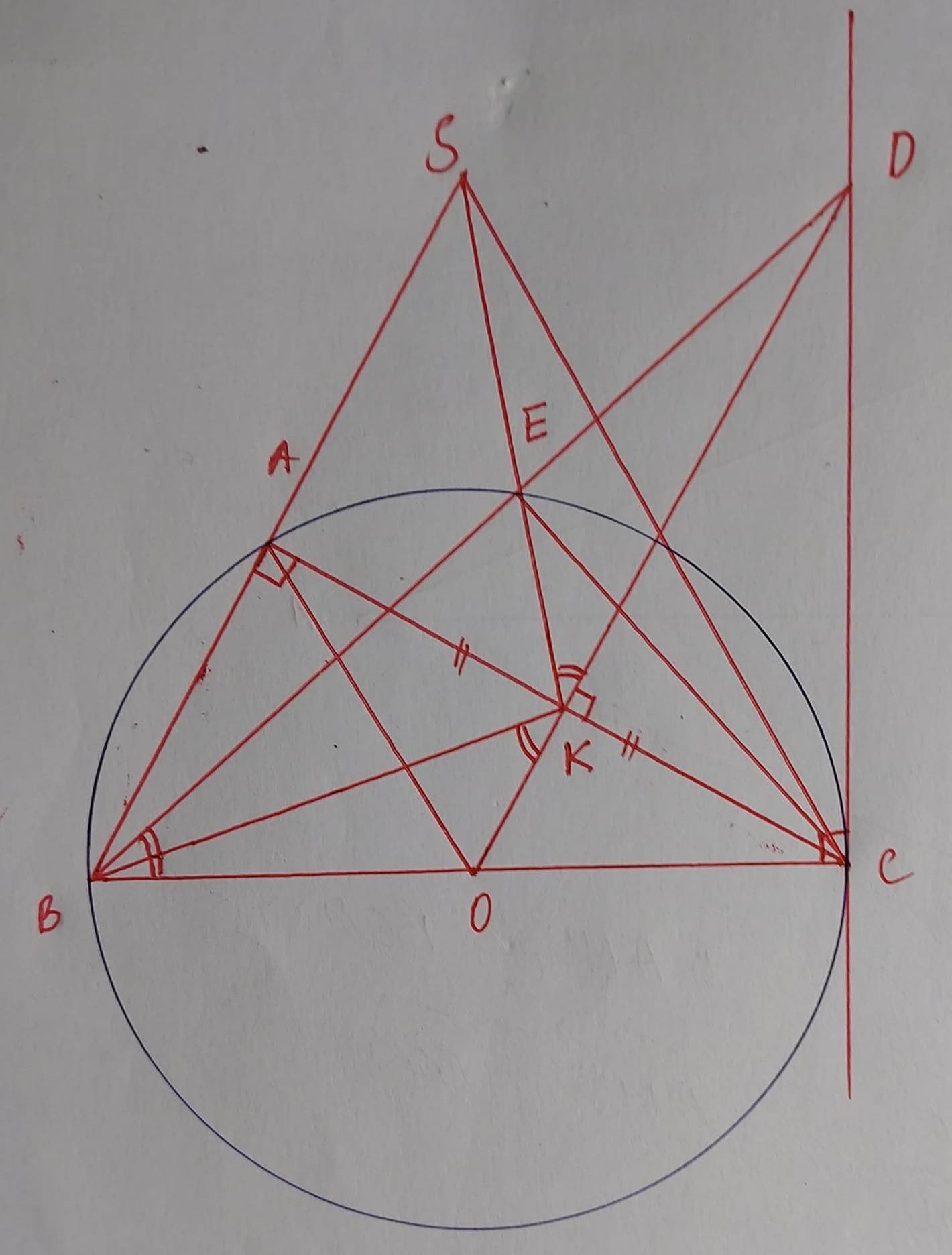
Bài toán: Cho ΔABC nội tiếp (O) có đường kính BC sao cho AB<AC. Gọi K là trung điểm của AC, tiếp tuyến tại C của (O) và tia OK cắt nhau ở D.
a) Chứng minh OK ⊥ AC,
b) BD cắt (O) tại E. Chứng minh DE.DB=DK.DO
c) Gọi S là giao điểm của tia KE và tia BA. Chứng minh OA//CS.
Giải:
Ta có DE.DB=DK.DO(cmt)
⇒ DE/DO=DK/DB
có góc BDO chung
⇒ tam giác DEK~DOB( c g c)
⇒ góc DKE=DBO(1)
áp dụng hệ thức lượng vào tam giác OCD vuông tại C có đường cao CK ta có:
OK.OD=OC^2=OB^2(Vì OB=OC=R)
⇒ OK/OB=OB/OD
có góc DOB chung
⇒ tam giác OKB~OBD( c g c)
⇒ góc OKB=DBO(2)
từ(1) và(2) suy ra góc DKE=OKB
mà góc DKE+AKS=OKB+AKB=90 độ
⇒ góc AKS=AKB
⇒ KA là tia phân giác của góc BKS
Chỉ ra KA vuông góc vs BS
⇒ tam giác KBS cân tại K
⇒ AB=AS
có OB=OC
⇒ OA là đường trung bình của tam giác BSC.
⇒ OA//CS( đpcm)