Bài toán: Cho ΔABC nhọn (AB<AC). Vẽ đường tròn (O) đường kính BC, đường tròn (O) cắt AB, AC lần lượt tại F, E. BE cắt CF tại H, AH cắt BC tại D. Vẽ HI ⊥ OA tại I.
a) Chứng minh: A, E, H, F cùng thuộc đường tròn, xác định tâm S.
b) Chứng minh AE.AC = AH.AD = Ai.AO
c) HI cắt (O) tại M. Chứng minh: AM là tiếp tuyến của (O).
Hướng dẫn giải:
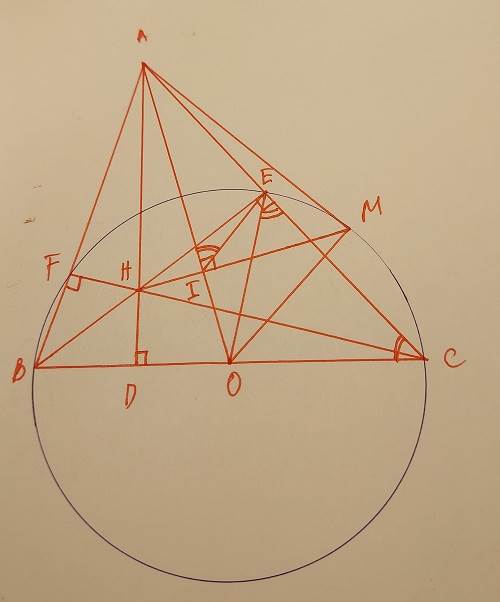
Ta có AI.AO=AE.AC( cmt)
⇒ AI/AC=AE/AO
có góc OAC chung
⇒ tam giác AIE~ACO( c g c)
⇒ góc AIE=ACO
xét( O) có OE=OC=R
⇒ tam giác OCE cân tại O
⇒ góc OCE=OEC
hay góc OCE=ACO
⇒ góc AIE=OCE(=ACO)
mà góc OIE+AIE=OEA+OCE=180 độ( kề bù)
⇒ góc OIE=OEA
chỉ ra tam giác OIE~OEA( g g)
⇒ OI/OE=OE/OA
⇒ OI.OA=OE^2=OM^2
⇒ OI/OM=OM/OA
góc AOM chung
⇒ tam giác OIM~OMA( c g c)
⇒ góc OMA=OIM=90 độ
⇒ AM vuông góc vs OM
⇒ AM là tiếp tuyến của(O) (đpcm)