Bài toán 1: Cho tam giác ABC có trung tuyến AM, đường thẳng song song với BC cắt AB và AC lần lượt tại E và F. Chứng minh AM đi qua trung điểm của EF.
Giải bằng kiến thức học kì 1 (hết chương 2) lớp 8. Không dùng định lý Talet và tam giác đồng dạng.
Giải:
Cách 1:
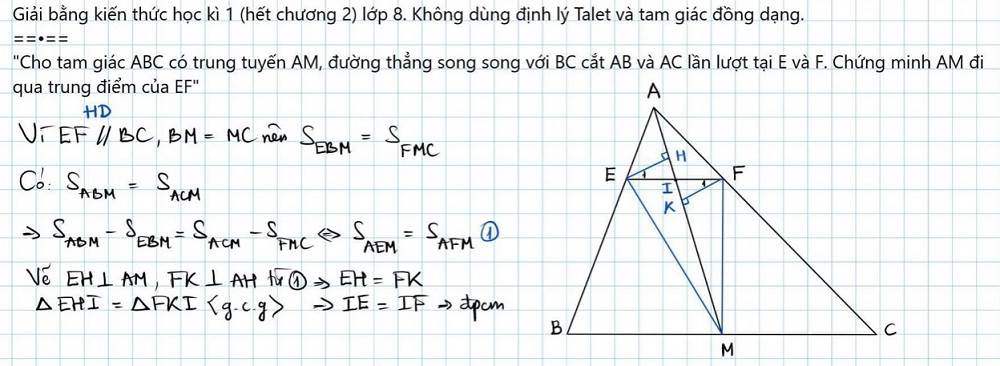
Cách 2:

Bài toán 2: Cho hình vuông ABCD. Gọi M, N lần lượt là trung điểm của AB, BC. Gọi H là giao điểm của DN và CM, E là giao điểm của AH với BC.
a. Chứng minh: DN ⊥ CM
b. Chứng minh: AD + CE = AE
c. Kẻ HK vuông góc với DC tại K, I là giao điểm của AC vói HK. Chứng minh: IH = IK
Giải:
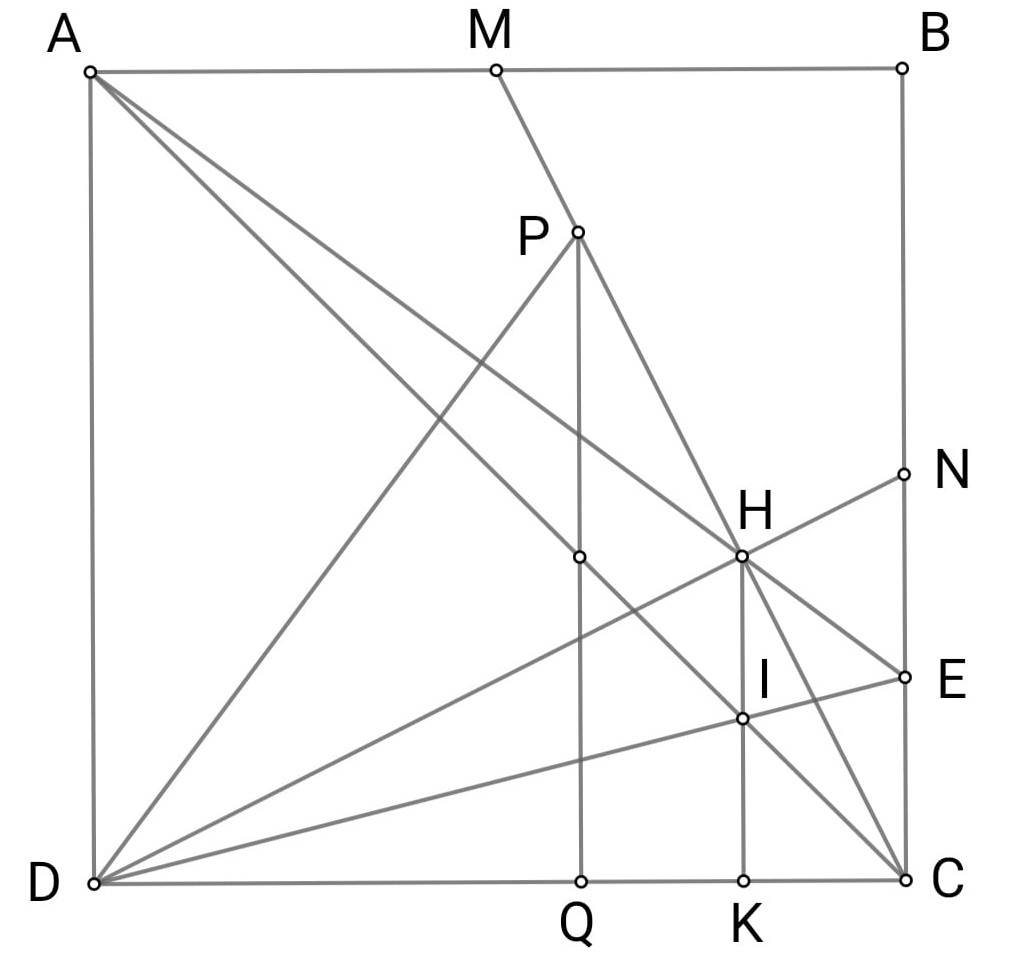
c. Gọi P, Q lần lượt là các điểm đối xứng với C qua H, K. ∆CPQ có HK là đường trung bình và vuông góc CQ nên ∆CPQ vuông tại Q
∆CDP có DH vừa là đường cao vừa là đường trung tuyến nên ∆CDP cân
Xét hai tam giác cân ADH và DCP, có AD = DC, góc AHD = EHN (đối đỉnh) = ENH (∆EHN cân) = DCP (phụ góc HCN)
=> ∆ADH = DCP (g.c.g)
=> DH = CP
Xét ∆DKH và ∆PQC, có:
DH = CP (cmt)
Góc DKH = PQC = 90°
Góc DHK = PCQ (phụ góc CHK)
Hoặc góc HDK = CPQ (góc tạo bởi các cạnh tương ứng vuông góc)
=> ∆DKH = ∆PQC (g.c.g)
=> HK = CQ
Mà ∆IKC vuông có góc KCI = 45° nên ∆IKC vuông cân
=> IK = KC = CQ/2 = HK/2
=> đpcm





phần b làm như thế nào Thế bài hình ý
Vì ∆HNC vuông tại H => HE = EC (1)
=> HE = NE => EHN cân => EHN = ENH
Vì AHD = NHE (đối đỉnh)
=> AHD = ENH mà AD // NE => END = ADN (so le trong)
=> AHD = ADN => ∆AHD cân => AD = AH (2)
Vì (1) và (2) => đpcm