Cho tam giác vuông có ba cạnh a, b, c là số nguyên.
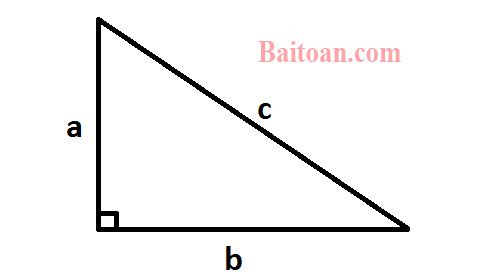
Tìm tất cả trường hợp của tam giác vuông này thỏa mãn điều kiện diện tích bằng hai lần chu vi tam giác?
Vì bài này khó quá nên Baitoan.com sẽ đưa ra lời giải ngay dưới đây:
Đáp án:
Đặt a, b là hai cạnh góc vuông và c là cạnh huyền của tam giác đã cho. Vì diện tích tam giác bằng hai lần chu vi, ta có:
ab/2 = 2(a + b + c)
ab/4 = a + b + c
(ab/4 – a – b)2 = c2
Theo Pytago ta có a2 + b2 = c2.
Suy ra (ab/4 – a – b)2 = a2 + b2
a2b2/16 + a2 + b2 + 2ab – a2b/2 – ab2/2 = a2 + b2
a2b2/16 – a2b/2 – ab2/2 + 2ab = 0
ab(ab/16 – a/2 – b/2 + 2) = 0
Vì ab ≠ 0 nên ta có ab – 8a – 8b + 32 = 0.
Hay ab – 8a – 8b + 64 – 32 = 0
a (b – 8) – 8(b – 8) = 32
(a – 8)(b – 8) = 32 = 1 x 32 = 8 x 4 = 2 x 16.
Các cặp (a – 8; b – 8) tương ứng là (1; 32), (8; 4), (2; 16).
Suy ra các cặp (a; b) tương ứng là (9; 40), (16; 12) và (10; 24). Từ đó suy ra c tương ứng trong các trường hợp lần lượt là 41; 20 và 26.
Vậy, các trường hợp của tam giác vuông có cạnh (a; b; c) thỏa mãn đề bài là
(9; 40; 41); (16; 12; 20) và (10; 24; 26).
Khó quá phải không nào các bạn :))








70 hình :]