Luật số lớn là một phần của Lý thuyết xác suất và thống kê. Trong thực tế, những hiện tượng ngẫu nhiên do rất nhiều nguyên nhân ngẫu nhiên gây ra. Việc tìm điều kiện để những hiện tượng như vậy xảy ra theo một quy luật nào đó là ý nghĩa của định lý luật số lớn.
Từ khi được chứng minh thành công thức, luật số lớn được áp dụng rất nhiều trong thực tế với các bài toán xác suất. Với các trò chơi may rủ như xổ số, luật số lớn cũng được áp dụng để tính khả năng trúng giải thưởng xsmn thứ 7 rất chính xác.
1/ Luật số lớn
Khái niệm tổng quát
Cho dãy các biến ngẫu nhiên X1, X2, …, Xn, … (2.1) Xét biến ngẫu nhiên Yn là một hàm đối xứng nào đó của n biến ngẫu nhiên đầu tiên của dãy (2.1):
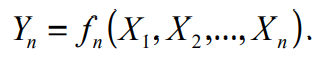
Nếu tồn tại một dãy các hằng số a1, a2, …, an, … sao cho với mọi ε dương:
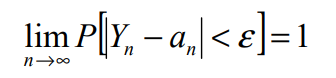
thì dãy (2.1) được gọi là tuân theo luật số lớn với hàm đã cho.
Dạng Chebyshev của luật số lớn.
- Định nghĩa
Ta nói họ biến ngẫu nhiên {Xn, n ≥ 1} tuân theo luật số lớn (dạng Chebyshev) nếu ∀ε > 0:
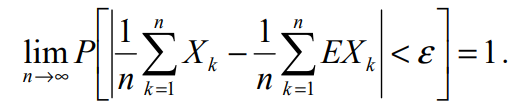
- Bất đẳng thức Chebyshev
Nếu biến ngẫu nhiên X có phương sai hữu hạn, thì bất đẳng thức sau đây được thỏa mãn với mọi ε > 0:
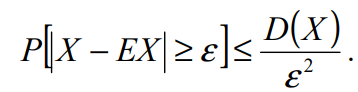
- Định lý Chebyshev
Nếu X1, X2, …, Xn,… là một dãy các biến ngẫu nhiên ñộc lập từng đôi một có phương sai hữu hạn và bị chặn bởi cùng một hằng số DXk ≤ C, ∀k thì với mọi hằng số ε > 0, ta luôn có:
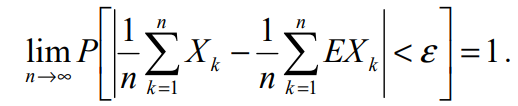
Điều kiện cần và đủ cho luật số lớn.
Định lý 2.3.1. Cho dãy biến ngẫu nhiên tùy ý X1, X2, …, Xn, … Điều kiện cần và đủ để dãy biến ngẫu nhiên này thỏa mãn hệ thức:
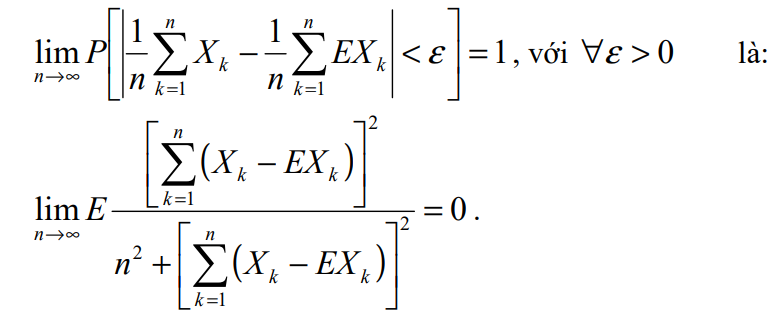
2/ Một số ứng dụng của luật số lớn
Luật số lớn được áp dụng nhiều nhất trong thống kê xác suất.
Tần suất xuất hiện biến cố trong n phép thử là tỷ số giữa số phép thử trong đó biến cố xuất hiện và tổng số phép thử ñược thực hiện. Nếu ký hiệu số phép thử là n, số lần xuất hiện biến cố A là n(A), tần suất xuất hiện biến cố A là:
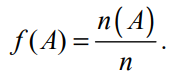
Khi số phép thử tăng lên vô hạn, tần suất xuất hiện biến cố tiến dần đến một số xác định, số đó được gọi là xác suất của biến cố đó. Hay nói cách khác, xác suất là giới hạn của tần suất khi số phép thử tăng lên vô hạn:
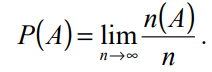
Tuy nhiên trong thực tế không thể tiến hành vô hạn phép thử, nhưng đối với số phép thử đủ lớn ta có thể xem xác suất xấp xỉ bằng tần suất:
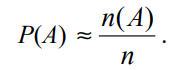
Nói một cách khác dễ hiểu. Khi ta thực hiện một thí nghiệm thành công với xác suất là P(A) và lập lại thí nghiệm này n lần, thì số lần thành công sẽ xấp xỉ n(A).
Như trong xổ số, nếu đài phụ xsmn thứ 4 là xổ số Long An có 10 triệu người mua vé, xác suất trúng giải độc đắc là 1 phần 1 triệu, thì trung bình sẽ có 10 người trúng giải. Điều này giải thích cho việc dù biết tỷ lệ trúng giải là rất nhỏ nhưng nhiều người vẫn mua vé số và mỗi người đều có tỷ lệ trúng thấp như nhau.