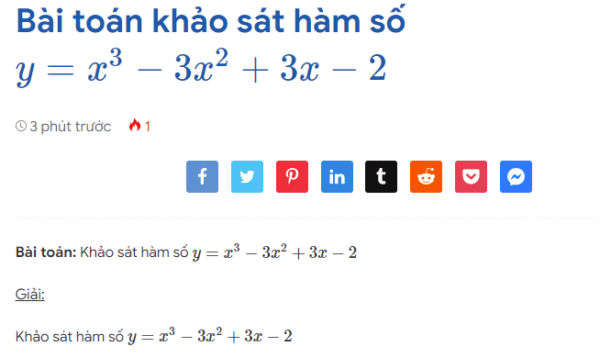Bài toán: Khảo sát hàm số $y=x^3+3x^2-4$. Hướng dẫn: Tập xác định: $D=\mathbb{R}$ Chiều biến thiên: Ta có: $ y\prime=3x^2+6x+0$ $ y\prime=0 \Leftrightarrow x=-2$ hoặc $ x=0$ Hàm số đồng biến trên các khoảng $(-\infty;-2)$ và $(0;+\infty)$, nghịch biến trên khoảng $(-2;0)$. Hàm số đạt cực đại tại điểm $ x= -2$, giá trị cực […]
Bài toán: Khảo sát hàm số $ \displaystyle y=\dfrac{{x+3}}{{x+1}}$ Giải: Tập xác định: $D=\mathbb{R}\backslash \{-1\}$ Ta có: $ y\prime=\dfrac {-2}{(x+1)^2}<0 \forall x \in D \Rightarrow$ hàm số nghịch biến trên các khoảng $(-\infty;-1)$ và $(-1;+\infty)$ Giới hạn, tiệm cận: $\lim\limits_{x\to +\infty } y=\lim\limits_{x\to -\infty } y=1\Rightarrow y=1$ là tiệm cận ngang của đồ thị hàm […]
Bài toán: Khảo sát hàm số $ \displaystyle y=\dfrac{{x-2}}{{x-1}}$ Giải: Tập xác định: $D=\mathbb{R}\backslash \{1\}$ Ta có: $ y\prime=\dfrac {1}{(x-1)^2}>0 \forall x \in D \Rightarrow$ hàm số đồng biến trên các khoảng $(-\infty;1)$ và $(1;+\infty)$ Giới hạn, tiệm cận: $\lim\limits_{x\to +\infty } y=\lim\limits_{x\to -\infty } y=1\Rightarrow y=1$ là tiệm cận ngang của đồ thị hàm […]
Bài toán: Khảo sát hàm số $ \displaystyle y=\dfrac{{x+1}}{{x-2}}$ Giải: Tập xác định: $D=\mathbb{R}\backslash \{2\}$ Ta có: $ y\prime=\dfrac {-3}{(x-2)^2}<0 \forall x \in D \Rightarrow$ hàm số nghịch biến trên các khoảng $(-\infty;2)$ và $(2;+\infty)$ Giới hạn, tiệm cận: $\lim\limits_{x\to +\infty } y=\lim\limits_{x\to -\infty } y=1\Rightarrow y=1$ là tiệm cận ngang của đồ thị hàm […]
Bài toán: Khảo sát hàm số $ \displaystyle y=\dfrac{{2x-1}}{{x-1}}$ Giải: Tập xác định: $D=\mathbb{R}\backslash \{1\}$ Ta có: $ y\prime=\dfrac {-1}{(x-1)^2}<0 \forall x \in D \Rightarrow$ hàm số nghịch biến trên các khoảng $(-\infty;1)$ và $(1;+\infty)$ Giới hạn, tiệm cận: $\lim\limits_{x\to +\infty } y=\lim\limits_{x\to -\infty } y=2\Rightarrow y=2$ là tiệm cận ngang của đồ thị hàm […]
Bài toán: Khảo sát hàm số $ \displaystyle y=\dfrac{{2x+1}}{{x-1}}$ Giải: Tập xác định: $D=\mathbb{R}\backslash \{1\}$ Ta có: $ y\prime=\dfrac {-3}{(x-1)^2}<0 \forall x \in D \Rightarrow$ hàm số nghịch biến trên các khoảng $(-\infty;1)$ và $(1;+\infty)$ Giới hạn, tiệm cận: $\lim\limits_{x\to +\infty } y=\lim\limits_{x\to -\infty } y=2\Rightarrow y=2$ là tiệm cận ngang của đồ thị hàm […]
Bài toán: Khảo sát hàm số $y=x^4+2x^2+3$ và $y=-x^4+2x^2+3$ Giải: Khảo sát hàm số $y=x^4+2x^2+3$ Tập xác định: $D=\mathbb{R}$ Chiều biến thiên: Ta có: $ y\prime=4x^3+4x$ $ y\prime=0 \Leftrightarrow x=0$ Hàm số đồng biến trên khoảng $(0;+\infty)$; nghịch biến trên khoảng $(-\infty;0)$ Hàm số đạt cực tiểu tại điểm $ x=0$, giá trị cực tiểu […]
Bài toán: Khảo sát hàm số $y=x^4-2x^2-3$ và $y=-x^4-2x^2-3$. Giải: Khảo sát hàm số $y=x^4-2x^2-3$ Tập xác định: $D=\mathbb{R}$ Chiều biến thiên: Ta có: $ y\prime=4x^3-4x$ $ y\prime=0 \Leftrightarrow x=0$ hoặc $ x=\pm1$ $ y\prime>0 \Leftrightarrow x \in (-1;0) \cup (1;+\infty)$; $ y\prime<0 \Leftrightarrow (-\infty;-1) \cup (0;1)$ Hàm số nghịch biến trên các khoảng $(-\infty;-1) […]
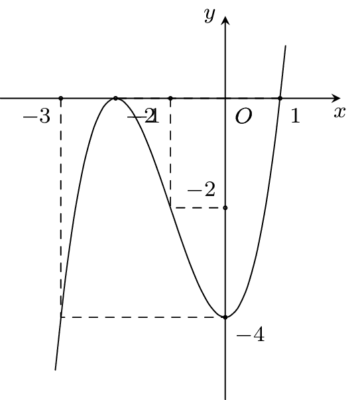
Bài toán: Khảo sát hàm số $y=x^3-3x^2+3x-2$ Giải: Khảo sát hàm số $y=x^3-3x^2+3x-2$ Tập xác định: $D=\mathbb{R}$ Chiều biến thiên: Ta có: $ y\prime=3x^2-6x+3$ $ y\prime \geq 0, \forall x \in \mathbb{R}$. Hàm số luôn đồng biến trên $\mathbb{R}$ Giới hạn của hàm số tại vô cực: $\lim\limits_{x\to -\infty } =-\infty$; $\lim\limits_{x\to +\infty } =+\infty$ […]
Bài toán: Khảo sát hàm số $y=x^3-3x+1$ và $y=-x^3-3x+1$. Giải: Khảo sát hàm số $y=x^3-3x+1$ Tập xác định: $D=\mathbb{R}$ Chiều biến thiên: Ta có: $ y\prime=3x^2+0x-3$ $ y\prime=0 \Leftrightarrow x=-1$ hoặc $ x=1$ Hàm số đồng biến trên các khoảng $(-\infty;-1)$ và $(1;+\infty)$, nghịch biến trên khoảng $(-1;1)$. Hàm số đạt cực đại tại điểm […]