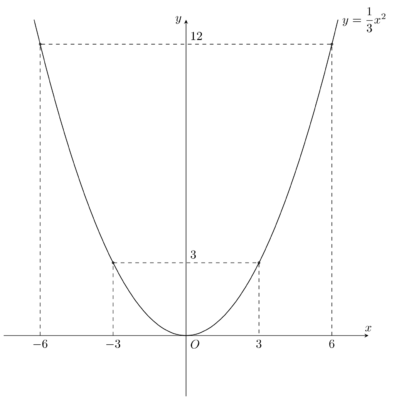
Bài tập: Khảo sát và vẽ đồ thị hàm số $y=\dfrac{1}{3}x^{2}$ (y=x^2/3) Giải: Khảo sát: Tập xác định: $ D=\mathbb{R}$ $ a=\dfrac{1}{3}>0$, hàm số đồng biến nếu $ x>0$, hàm số nghịch biến nếu $ x<0$ Vẽ đồ thị hàm số: Bảng giá trị hàm số y=1/3x^2 $ x$ ${-6}$ ${-3}$ ${0}$ ${3}$ ${6}$ $ […]
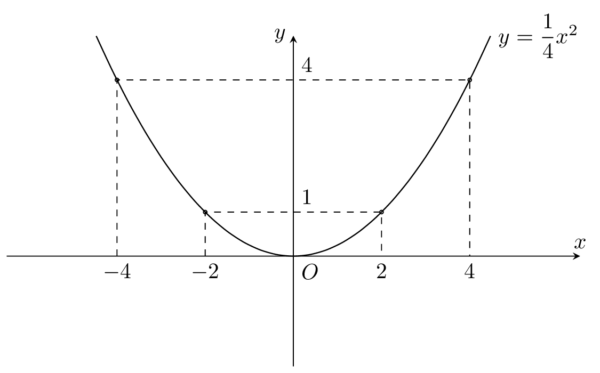
Bài toán: Khảo sát và vẽ đồ thị hàm số $ y=\dfrac {1}{4}x^2$ (y = -x^2) Giải: Khảo sát: Tập xác định: $D=\mathbb{R}$ $ a= \dfrac {1}{4}>0$, hàm số đồng biến nếu $ x>0$, hàm số nghịch biến nếu $ x<0$ Vẽ đồ thị hàm số: Bảng giá trị $ x$ ${-4}$ ${-2}$ ${0}$ ${2}$ […]
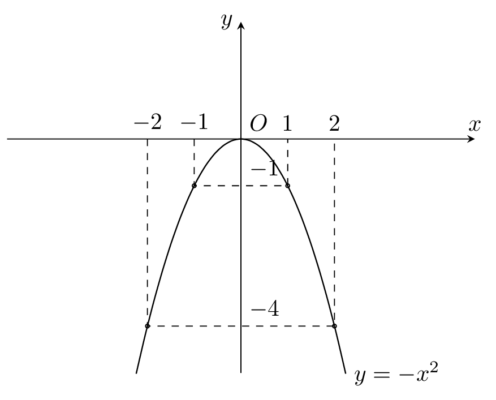
Bài toán: Khảo sát và vẽ đồ thị hàm số y = -x^2 Giải: Khảo sát: Tập xác định: $D=\mathbb{R}$ $ a= -1<0$, hàm số đồng biến nếu $ x<0$, hàm số nghịch biến nếu $ x>0$ Vẽ đồ thị hàm số: Bảng giá trị $ x$ ${-2}$ ${-1}$ ${0}$ ${1}$ ${2}$ $ y=-x^2$ ${-4}$ […]
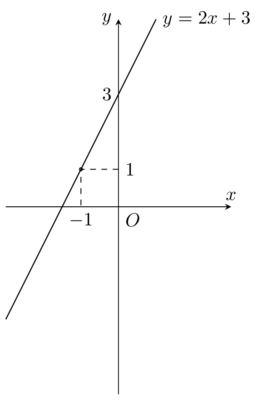
Bài toán: Khảo sát và vẽ đồ thị hàm số y = 2x +3 Giải: Khảo sát: Tập xác định: $D=\mathbb{R}$ $ a= 2>0$ nên hàm số đồng biến trên $\mathbb{R}$ Vẽ đồ thị hàm số: y = 2x +3 x = 0 ⇒ y = 3 x = -1 ⇒ y = 1 Đồ […]
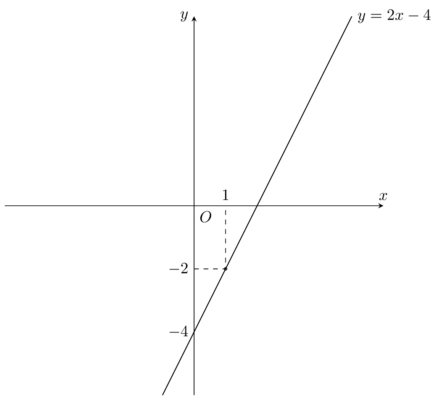
Bài toán: Khảo sát và vẽ đồ thị hàm số y = 2x – 4 Giải: Khảo sát: Tập xác định: $D=\mathbb{R}$ $ a= 2>0$ nên hàm số đồng biến trên $\mathbb{R}$ Vẽ đồ thị hàm số: y = 2x – 4 x = 0 ⇒ y = -4 x = 1 ⇒ y = […]
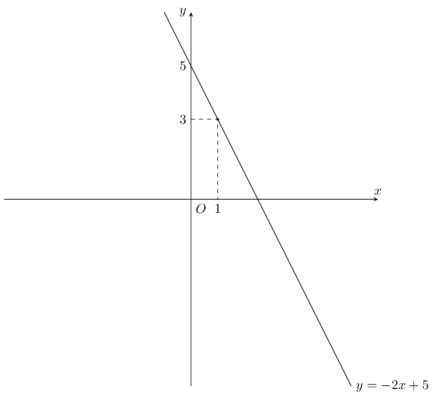
Bài toán: Khảo sát và vẽ đồ thị hàm số y = -2x + 5 Giải: Khảo sát: Tập xác định: $D=\mathbb{R}$ $ a= -2<0$ nên hàm số nghịch biến trên $\mathbb{R}$ Vẽ đồ thị hàm số: y = -2x + 5 x = 0 ⇒ y = 5 x = 1 ⇒ y = […]
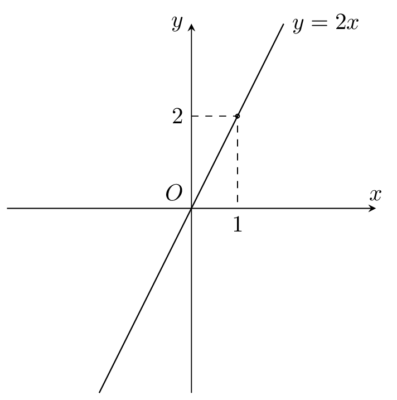
Bài toán: Vẽ đồ thị hàm số y = 2x Giải: y = 2x. x = 0 ⇒ y = 0 x = 1 ⇒ y = 2 Đồ thị hàm số $y= 2x$ là đường thẳng đi gốc tọa độ $O(0;0)$ và điểm $(1;2)$
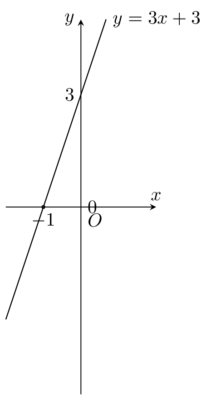
Bài toán: Khảo sát và vẽ đồ thị hàm số y = 3x + 3 Giải: Tập xác định: $D=\mathbb{R}$ $ a= 3>0$ nên hàm số đồng biến trên $\mathbb{R}$ Vẽ đồ thị hàm số y = 3x + 3: y = 3x + 3 x = 0 ⇒ y = 3 x = -1 […]
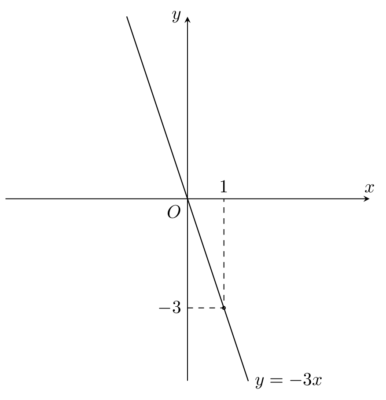
Bài toán: Vẽ đồ thị hàm số y = -3x Giải: y = -3x. x = 0 ⇒ y = 0 x = 1 ⇒ y = -3 Đồ thị hàm số $y= -3x$ là đường thẳng đi gốc tọa độ $O(0;0)$ và điểm $(1;-3)$
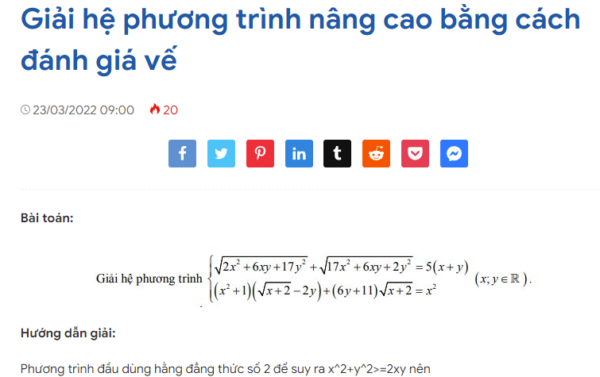
Bài toán: Hướng dẫn giải: Phương trình đầu dùng hằng đẳng thức số 2 để suy ra x^2+y^2>=2xy nên 2x^2+6xy+17y^2>=x^2+8xy+16y^2=(x+4y)^2 rồi đưa ra ngoài dấu căn, căn thứ hai làm tương tự sẽ được vế trái>=vế phải nên để hệ phương trình có nghiệm thì x=y. Thay vào phương trình 2 và giải là xong.