MỤC LỤC BÀI VIẾT
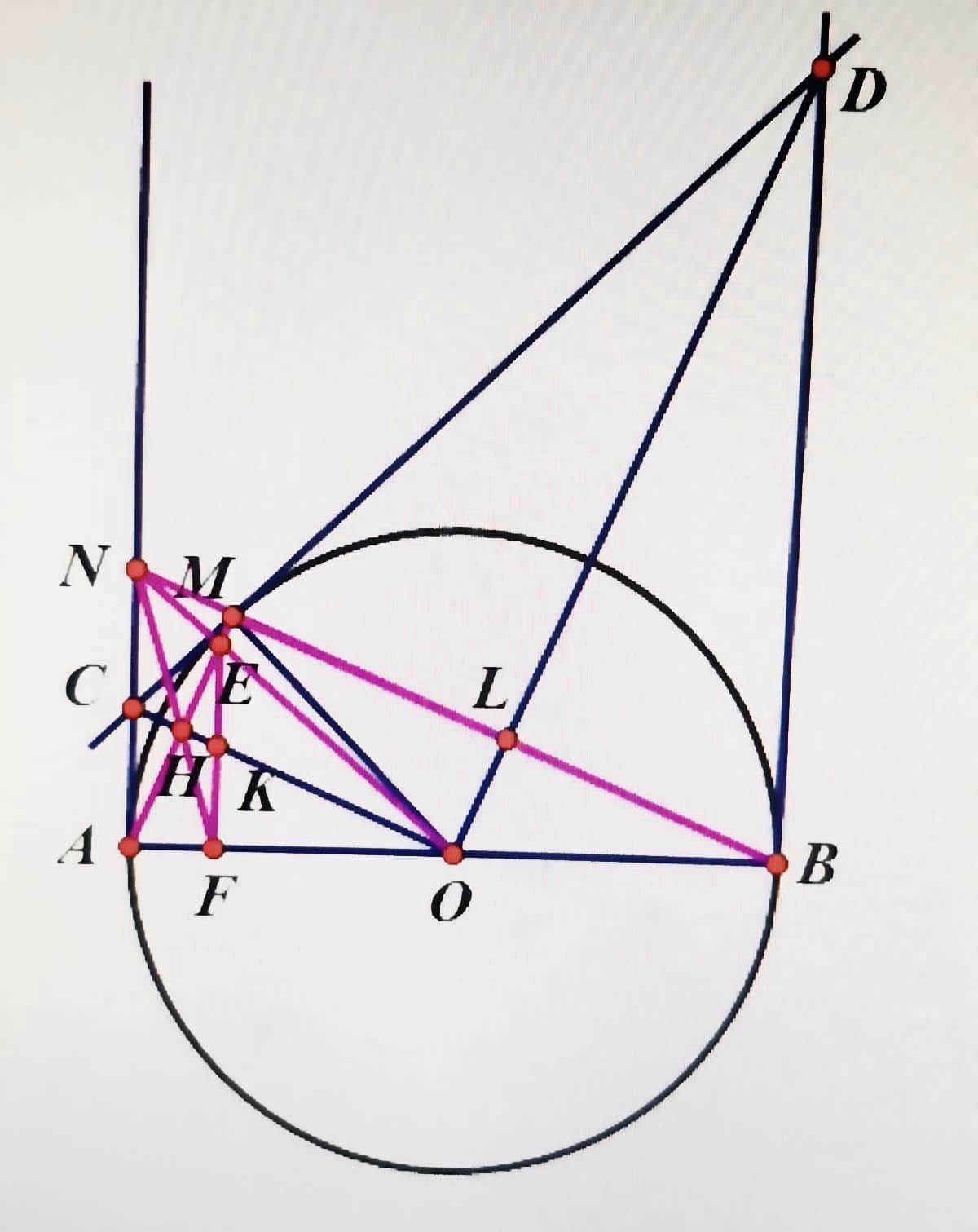
Bài toán: Cho nửa đường tròn (O;R) có AB là đường kính. Vẽ các tiếp tuyến Ax, By của nửa đường tròn (O;R). Trên nửa đường tròn (O;R) lấy điểm M (MA<MB). Tiếp tuyến tại M của nửa đường tròn (O;R) cắt Ax tại C và By tại D.
a) Chứng minh: CD= AC+BD
b) Chứng minh: góc COD= 90 độ và AC.BD= R^2
c) Đường thẳng BM cắt Ax tại N, AM cắt ON tại E và cắt OC tại H. Đường thẳng NH cắt AB tại F. K là giao điểm của OC và EF. Chứng minh: AN^2= NM. NB và KE= KF
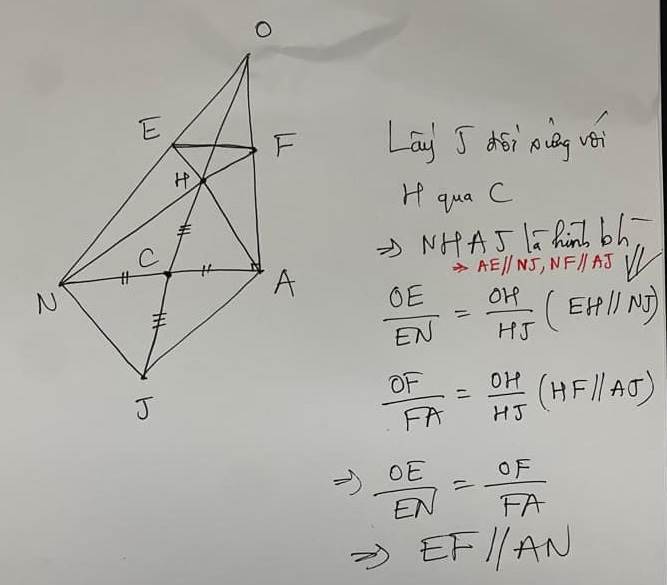
Hướng dẫn giải
