Trung học cơ sở

Bài toán: Lớp 6A quyên góp được một số sách để tặng các bạn học sinh ở trên vùng cao. Biết rằng nếu chia số sách đó thành từng thùng 10 cuốn, 12 cuốn hoặc 15 cuốn thì vừa đủ. Và số lượng sách nằm trong khoảng từ 200 đến 300 cuốn. Tìm số sách? […]

20 bài toán thực tế chọn lọc lớp 8 gồm: ứng dụng diện tích đa giác, ứng dụng tứ giác dành cho học sinh lớp 8 tự giải, luyện tập giải Toán.

Bài toán: Chứng minh tích của 4 số tự nhiên liên tiếp cộng với 1 là một số chính phương. Giải: Gọi 4 số tự nhiên liên tiếp là n , n + 1 , n + 2 , n + 3 . Khi đó ta có: Tích của 4 số tự nhiên liên tiếp […]

Bài toán: Cho $ \displaystyle \frac{a}{b}=\frac{c}{d}$ chứng minh rằng: $ \displaystyle \frac{5 a+3 b}{5 a-3 b}=\frac{5 c+3 d}{5 c-3 d}$ $ \displaystyle \frac{a \cdot c}{b \cdot d}=\frac{a^{2}+c^{2}}{b^{2}+d^{2}}$ Giải: Hướng dẫn: biến đổi tương đương về dãy tỉ số đã cho.

Bài tập: Tìm x thuộc số nguyên sao cho $A$ là số nguyên tố $A=x^{4}-6 x^{3}+12 x^{2}-12 x+20$ Giải: $A=x^{4}+2 x^{2}-6 x^{3}=12 x+10 x^{2}+20$ $A=x^{2}\left(x^{2}+2\right)-6 x\left(x^{2}+2\right)+10\left(x^{2}+2\right)$ $A=\left(x^{2}+2\right)\left(x^{2}-6 x+10\right)$ $A$ là số nguyên tố ⇒ $A = 1.P$ mà $x^{2}+2 \neq 1 \Rightarrow x^{2}-6 x+10=1$ ⇒ $ \displaystyle x=3$ ⇒ $ \displaystyle A={{x}^{2}}+2=11$ ⇒ $ \displaystyle […]

Một số bất đẳng thức thường dùng ở các lớp 6, 7, 8, 9 đã được chứng, áp dụng để để giải các bài tập BĐT trong chương trình Toán THCS. Các bất đẳng thức đó là: 1. Bất đẳng thức AM-GM (Arithmetic Means – Geometric Means): Với các bộ số $ \displaystyle{{a}_{1}};{{a}_{2}};…;{{a}_{n}}$ không âm […]

Những bài toán giải phương trình vô tỉ (vô tỷ) ở lớp 9 thường có nhiều cách giải. Trong bài viết này Baitoan.com chia sẻ 2 cách thường dùng nhất. Các em theo dõi ví dụ dưới đây. Ví dụ: Giải phương trình sau $ \displaystyle {(4x-1)\sqrt{{{{x}^{2}}+1}}=2{{x}^{2}}+2x+1}$ TXĐ = {R} Hướng giải: Với phương trình […]

Bài toán: Tìm số vừa là bội của 3 vừa là ước của 54? Đây là dạng toán cơ bản trong chương trình số học 6. Các số chia hết cho số a thì là bội của số a. Số b chia hết cho những số nào thì các số đó là ước của b. […]

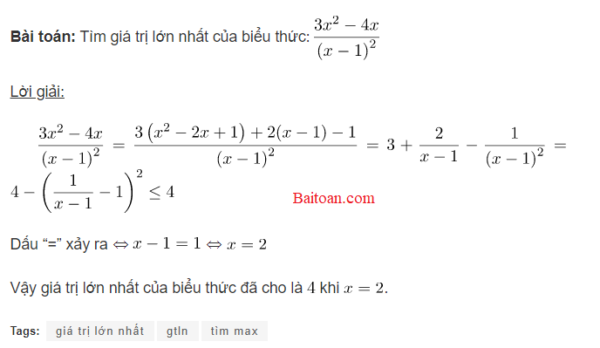
Bài toán: Tìm giá trị lớn nhất của biểu thức: $ \displaystyle \frac{{3{{x}^{2}}-4x}}{{{{{(x-1)}}^{2}}}}$ Lời giải: $ \displaystyle \frac{{3{{x}^{2}}-4x}}{{{{{(x-1)}}^{2}}}}=\frac{{3\left( {{{x}^{2}}-2x+1} \right)+2(x-1)-1}}{{{{{(x-1)}}^{2}}}}=3+\frac{2}{{x-1}}-\frac{1}{{{{{(x-1)}}^{2}}}}=4-{{\left( {\frac{1}{{x-1}}-1} \right)}^{2}}\le 4$ Dấu “=” xảy ra ⇔ $x – 1 = 1$ ⇔ $x = 2$ Vậy giá trị lớn nhất của biểu thức đã cho là $4$ khi $x = 2$.

Bài toán: Tìm số tự nhiên a biết a là số nhỏ nhất chia cho 9 dư 3, chia cho 27 dư 12, chia cho 41 dư 27. Giải: Ta có: a : 9 dư 3 => a – 3 chia hết cho 9 => a + 96 chia hết cho 9 a : 27 […]