Baitoan.com chia sẻ tới các bạn cách áp dụng dấu hiệu chia hết đã học ở lớp 4 để giải một bài toán khó. Trong bài viết này là dấu hiệu chia hết cho 5 và 9.
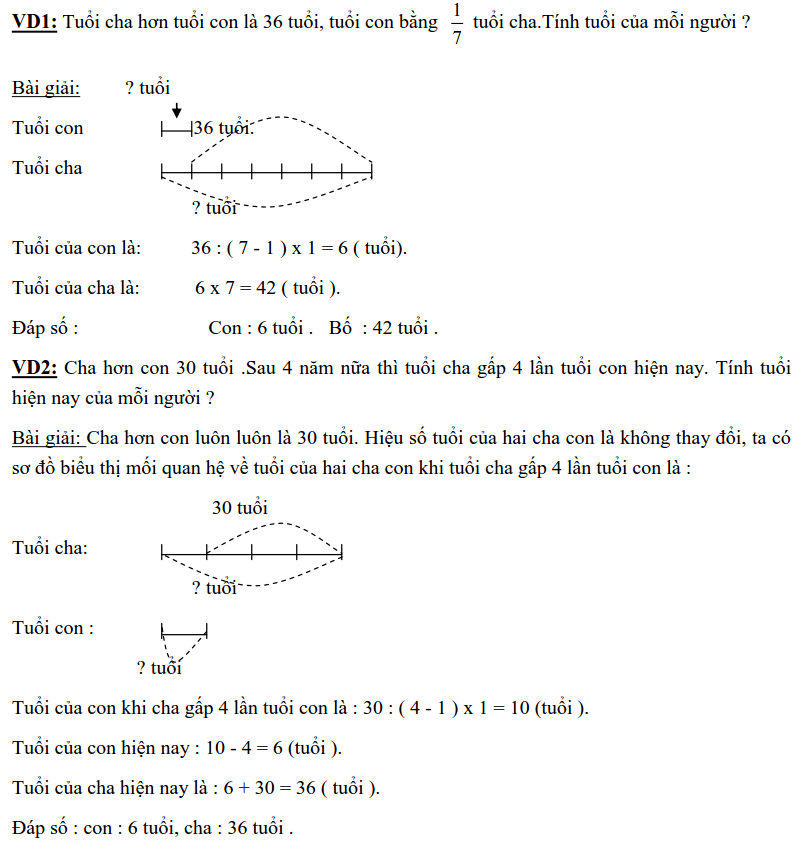
Bài toán: Tìm số có 5 chữ số $ \displaystyle \overline{{\text{abcde}}}$. Biết $ \displaystyle \overline{{\text{abcde}}}=\text{a }\!\!\times\!\!\text{ b }\!\!\times\!\!\text{ c }\!\!\times\!\!\text{ d }\!\!\times\!\!\text{ e}\times 45$.
Giải:
Lưu ý rằng 45 chia hết cho 9. Nên $ \displaystyle \overline{{\text{abcde}}}$ chia hết cho 9
Vậy (a + b + c + d + 5) phải chia hết cho 9
Mà a; b; c; d đều lẻ nên tổng a + b + c + d là số chẵn. Từ đó suy ra: a + b + c + d chỉ có thể nhận hai giá trị 4 hoặc 22
Xét lần lượt từng trường hợp
+ Nếu a + b + c + d = 4 thì chỉ có duy nhất 1 khả năng xảy ra: a = b = c = d = 1. Thử vào ta thấy không thỏa mãn nên loại
+ Trường hợp 2: nếu a + b + c + d = 22 thì chỉ có 2 khả năng đó là các chữ số (1; 5; 7; 9) hoặc (1; 7; 7; 7)
Thay vào thấy chỉ có 1 trường hợp thỏa mãn
Tìm đc số là 77175
(Theo Trần Trí Tuệ)