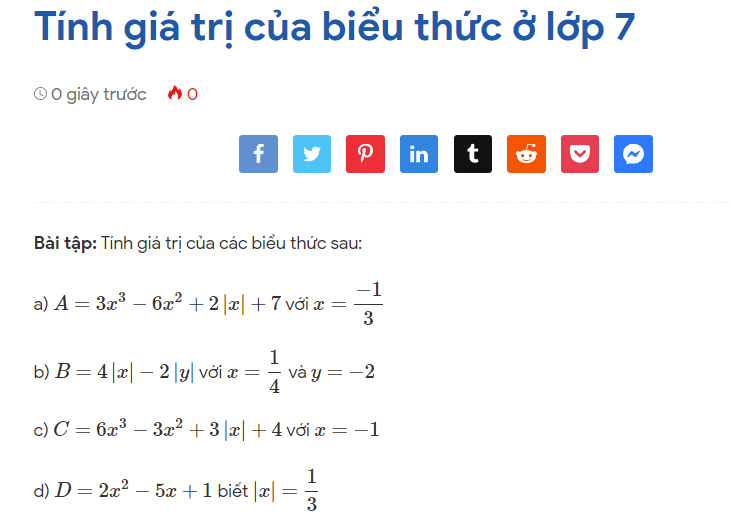
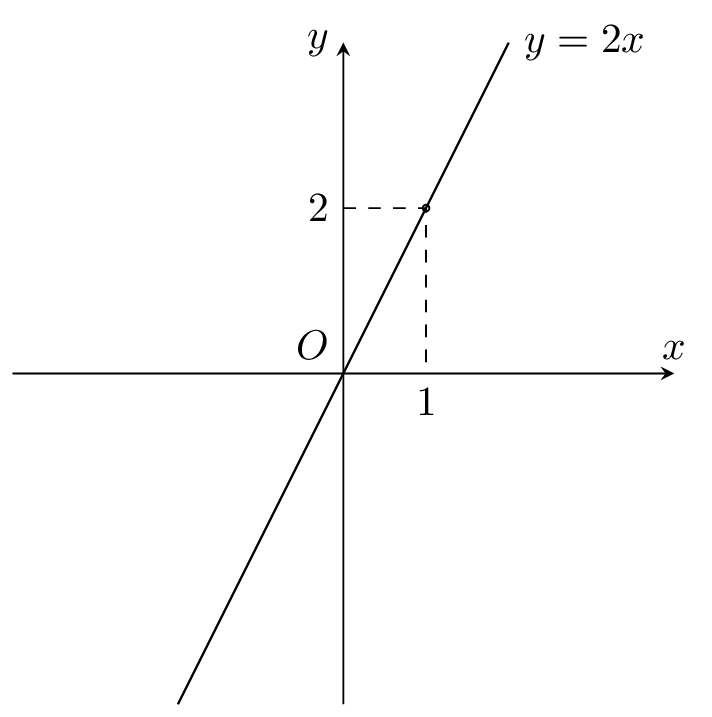
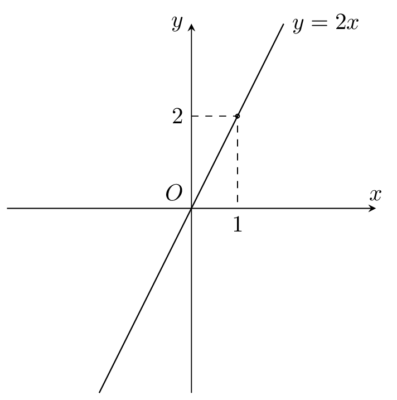
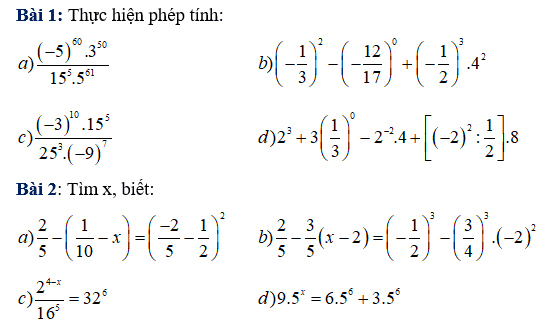Bài toán:
Cho góc xAy ( khác góc bẹt), Az là tia phân giác của góc xAy, B là điểm cố định trên Ax, C là điểm chuyển động trên đoạn AB, D là điểm chuyển động trên tia Ay sao cho AD=BC. CHứng minh rằng đường trung trực của CD luôn đi qua một điểm cố định khi C và D chuyển động.
P/s: Chỉ dùng kiến thức lớp 7 tới bài Trường hợp tam giác bằng nhau thứ 3 (g.c.g).
Xem đáp án (click):
Gọi M, N là trung điểm AB, CD và O là giao của trung trực của AB với Az. tgOMA = tgOMB (c.g.c.) => OA = OB => tgOAD = tgOBC (c.g.c.) => OD = OC => tgOND = tgONC (c.c.c) => ON là trung trực của CD => trung trực của CD đi qua O cố định.