Một số bất đẳng thức thường dùng ở các lớp 6, 7, 8, 9 đã được chứng, áp dụng để để giải các bài tập BĐT trong chương trình Toán THCS.
Các bất đẳng thức đó là:
1. Bất đẳng thức AM-GM (Arithmetic Means – Geometric Means):
Với các bộ số $ \displaystyle{{a}_{1}};{{a}_{2}};…;{{a}_{n}}$ không âm ta có:
$ \displaystyle\frac{{{{a}_{1}}+{{a}_{2}}+…+{{a}_{n}}}}{n}\ge \sqrt[n]{{{{a}_{1}}{{a}_{2}}…{{a}_{n}}}}$
Ta có 3 dạng thường gặp của bđt này là.
Dạng 1: $ \displaystyle \frac{{{{a}_{1}}+{{a}_{2}}+…+{{a}_{n}}}}{n}\ge \sqrt[n]{{{{a}_{1}}{{a}_{2}}…{{a}_{n}}}}$
Dạng 2: $ \displaystyle {{a}_{1}}+{{a}_{2}}+…+{{a}_{n}}\ge n\sqrt[n]{{{{a}_{1}}{{a}_{2}}…{{a}_{n}}}}$
Dạng 3: $ \displaystyle {{\left( {\frac{{{{a}_{1}}+{{a}_{2}}+…+{{a}_{n}}}}{n}} \right)}^{n}}\ge {{a}_{1}}{{a}_{2}}…{{a}_{n}}$
Dấu “=” xảy ra khi $ \displaystyle {{a}_{1}}={{a}_{2}}=…{{a}_{n}}$
Đối với BĐT này ta cần thành thạo kĩ thuật sử dụng bđt AM-GM cho 2 số và 3 số
2. Bất đẳng thức Cauchy-Schwarz (Bunyakovsky)
Dạng tổng quát: Cho $ \displaystyle {{a}_{1}};{{a}_{2}};…{{a}_{n}};{{b}_{1}};{{b}_{2}};…{{b}_{n}}$ là 2n số thực tùy ý khi đó
Dạng 1: $ \displaystyle (a_{1}^{2}+…+a_{n}^{2})(b_{1}^{2}+…+b_{n}^{2})\ge {{({{a}_{1}}{{b}_{1}}+…+{{a}_{n}}.{{b}_{n}})}^{2}}$ (1)
Dạng 2: $ \displaystyle \sqrt{{(a_{1}^{2}+…+a_{n}^{2})(b_{1}^{2}+…+b_{n}^{2})}}\ge |{{a}_{1}}{{b}_{1}}+…+{{a}_{n}}.{{b}_{n}}|$ (2)
Dạng 3: $ \displaystyle \sqrt{{(a_{1}^{2}+…+a_{n}^{2})(b_{1}^{2}+…+b_{n}^{2})}}\ge {{a}_{1}}{{b}_{1}}+…+{{a}_{n}}.{{b}_{n}}$ (3)
Dấu “=” xảy ra ở (1)(2) $ \displaystyle \Leftrightarrow \frac{{{{a}_{1}}}}{{{{b}_{1}}}}=…=\frac{{{{a}_{n}}}}{{{{b}_{n}}}}$
Dấu “=” xảy ra ở (3) $ \displaystyle \Leftrightarrow \frac{{{{a}_{1}}}}{{{{b}_{1}}}}=…=\frac{{{{a}_{n}}}}{{{{b}_{n}}}}\ge 0$
Quy ước mẫu bằng 0 thì tử bằng 0
3. Bất đẳng thức Cauchy-Schwarz dạng Engel hay còn gọi là BĐT Schwarz
Cho $ \displaystyle {{a}_{1}};{{a}_{2}};…{{a}_{n}};{{b}_{1}};{{b}_{2}};…{{b}_{n}}$ là các số >0
Ta có: $ \displaystyle \frac{{x_{1}^{2}}}{{{{a}_{1}}}}+\frac{{x_{2}^{2}}}{{{{a}_{2}}}}+…+\frac{{x_{n}^{2}}}{{{{a}_{n}}}}\ge \frac{{{{{({{x}_{1}}+{{x}_{2}}+…+{{x}_{n}})}}^{2}}}}{{{{a}_{1}}+{{a}_{2}}+…+{{a}_{n}}}}$
Dấu “=” xảy ra khi $ \displaystyle \frac{{{{x}_{1}}}}{{{{a}_{1}}}}=\frac{{{{x}_{2}}}}{{{{a}_{2}}}}…=\frac{{{{x}_{n}}}}{{{{a}_{n}}}}$
4. Bất đẳng thức Chebyshev (Trê- bư-sép)
Dạng tổng quát
Nếu $ \displaystyle \left\{ {\begin{array}{*{20}{l}} {{{a}_{1}}\ge {{a}_{2}}\ge …\ge {{a}_{n}}} \\ {{{b}_{1}}\ge {{b}_{2}}\ge …\ge {{b}_{n}}} \end{array}} \right.$
Hoặc $ \displaystyle \left\{ {\begin{array}{*{20}{l}} {{{a}_{1}}\le {{a}_{2}}\le …\le {{a}_{n}}} \\ {{{b}_{1}}\le {{b}_{2}}\le …\ge {{b}_{n}}} \end{array}} \right.$
Dạng 1:
$ \displaystyle \frac{{{{a}_{1}}.{{b}_{1}}+{{a}_{2}}.{{b}_{2}}+…+{{a}_{n}}.{{b}_{n}}}}{n}\ge \frac{{{{a}_{1}}+{{a}_{2}}+…+{{a}_{n}}}}{n}.\frac{{{{b}_{1}}+{{b}_{2}}+…+{{b}_{n}}}}{n}$
Dạng 2:
$ \displaystyle n({{a}_{1}}{{b}_{1}}+{{a}_{2}}{{b}_{2}}+…+{{a}_{n}}{{b}_{n}})\ge ({{a}_{1}}+{{a}_{2}}+…+{{a}_{n}})({{b}_{1}}+{{b}_{2}}+…+{{b}_{n}})$
Nếu $ \displaystyle \left\{ {\begin{array}{*{20}{l}} {{{a}_{1}}\le {{a}_{2}}\le …\le {{a}_{n}}} \\ {{{b}_{1}}\ge {{b}_{2}}\ge …\ge {{b}_{n}}} \end{array}} \right.$
hoặc $ \displaystyle \left\{ {\begin{array}{*{20}{l}} {{{a}_{1}}\ge {{a}_{2}}\ge …\ge {{a}_{n}}} \\ {{{b}_{1}}\le {{b}_{2}}\le …\le {{b}_{n}}} \end{array}} \right.$
Dạng 1:
$ \displaystyle \frac{{{{a}_{1}}.{{b}_{1}}+{{a}_{2}}{{b}_{2}}+…+{{a}_{n}}.{{b}_{n}}}}{n}\le \frac{{{{a}_{1}}+{{a}_{2}}+…+{{a}_{n}}}}{n}.\frac{{{{b}_{1}}+{{b}_{2}}+…+{{b}_{n}}}}{n}$
Dạng 2:
$ \displaystyle n({{a}_{1}}{{b}_{1}}+{{a}_{2}}{{b}_{2}}+…+{{a}_{n}}{{b}_{n}})\le ({{a}_{1}}+{{a}_{2}}+…+{{a}_{n}})({{b}_{1}}+{{b}_{2}}+…+{{b}_{n}})$
Bất đẳng thức Chebyshev không được sử dụng trực tiếp mà phải chứng minh lại bằng cách xét hiệu
Bất đẳng thức Chebyshev cho dãy số sắp thứ tự, do đó nếu các số chưa sắp thứ tự ta phải giả sử có quan hệ thứ tự giữa các số.
5. Bất đẳng thức Bernoulli
Với $ \displaystyle x>-1;r\ge 1\vee r\le 0\Rightarrow {{(1+x)}^{r}}\ge 1+rx$
Nếu $ \displaystyle 1>r>0$ thì $ {{(1+x)}^{r}}\le 1+rx$
Bất đẳng thức này có thể chứng minh bằng phương pháp quy nạp hoặc sử dụng BĐT AM-GM
6. Bất đẳng thức Netbitt
Ở đây mình chỉ nêu dạng thường dùng
Với x,y,z là các số thực >0
Bất đẳng thức Netbitt 3 biến:
$ \displaystyle \frac{x}{{y+z}}+\frac{z}{{x+y}}+\frac{y}{{x+z}}\ge \frac{3}{2}$
Dấu “=” xảy ra khi x=y=z>0
BĐT Netbitt 4 biến:
$ \displaystyle \frac{a}{{b+c}}+\frac{b}{{d+c}}+\frac{c}{{d+a}}+\frac{d}{{a+b}}\ge 2$
Dấu “=” xảy ra khi a=b=c=d>0
7. Bất đẳng thức trung bình cộng – trung bình điều hòa AM-HM (Arithmetic Means – Hamonic Means)
Nếu $ {{a}_{1}},{{a}_{2}},…,{{a}_{n}}$ là những số thực dương thì
$ \displaystyle \frac{{{{a}_{1}}+{{a}_{2}}+…+{{a}_{n}}}}{n}\ge \frac{n}{{\frac{1}{{{{a}_{1}}}}+\frac{1}{{{{a}_{2}}}}+…+\frac{1}{{{{a}_{n}}}}}}$
Dấu “=” xảy ra khi $ {{a}_{1}}={{a}_{2}}=…={{a}_{n}}$
8. Bất đẳng thức Schur
Dạng thường gặp
Cho a,b,c là những số không âm
$ (a+b-c)(b+c-a)(c+a-b)\le abc$
$ {{a}^{r}}(a-b)(a-c)+{{b}^{r}}(b-a)(b-c)+{{c}^{r}}(c-a)(c-b)\ge 0$ với r là số thực dương
Đẳng thức xảy ra khi a=b=c hoặc a=0 và b=c và các hoán vị
9. Bất đẳng thức chứa dấu giá trị tuyệt đối
Với mọi số thực x,y ta có $ |x+y|\le |x|+|y|$
Đẳng thức xảy ra khi x,y cùng dấu hay $ xy\ge 0$
Với mọi số thực x,y ta có $ |x-y|\ge |x|-|y|$
Dấu “=” xảy ra khi và chỉ khi $ y(x-y)\ge 0$
10. Bất đẳng thức Mincopxki
Với 2 bộ n số $ {{a}_{1}},{{a}_{2}},…,{{a}_{m}}$ và $ {{b}_{1}},{{b}_{2}},…,{{b}_{m}}$ thì :
Dạng 1:
$\sqrt{a_{1}^{2}+b_{1}^{2}}+\sqrt{a_{2}^{2}+b_{2}^{2}}+\ldots+\sqrt{a_{m}^{2}+b_{m}^{2}} \geq \sqrt{\left(a_{1}+a_{2}+\ldots+a_{m}\right)^{2}+\left(b_{1}+b_{2}+\ldots+b_{m}\right)^{2}}$
Dạng 2: Cho x,y,z,a,b,c là các số dương ta có
$\sqrt[4]{a b c}+\sqrt[4]{x y z} \leq \sqrt[4]{(a+x)(b+y)(c+z)} \sqrt{a c}+\sqrt{b d} \leq \sqrt{(a+b)(c+d)}$

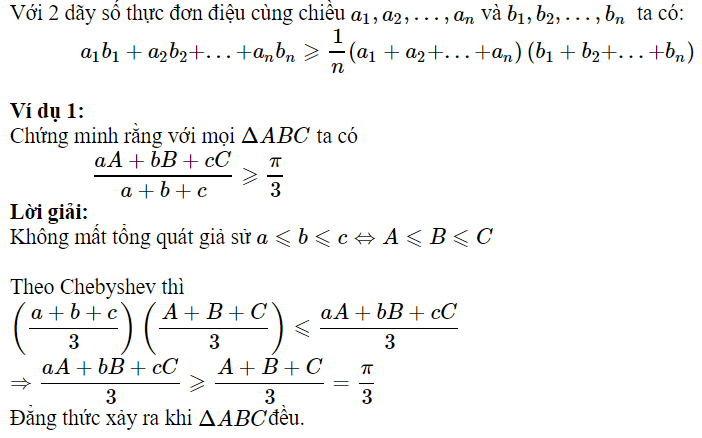





ờm, cái này hơi khó hiểu, nên cho thêm ví dụ nữa