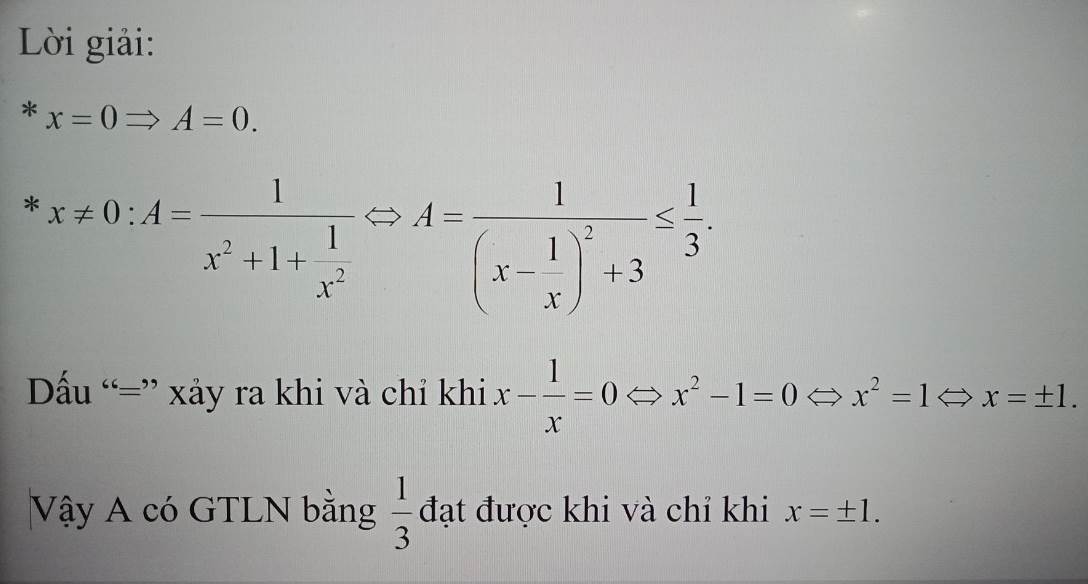7 hằng đẳng thức đáng nhớ
1) $ \displaystyle (A+B)^{2}=A^{2}+2AB+B^{2}$
2) $ \displaystyle (A-B)^{2}=A^{2}-2AB+B^{2}$
3) $ \displaystyle A^{2}-B^{2}=(A-B)(A+B)$
4) $ \displaystyle (A+B)^{3}=A^{3}+3A^{2}B+3AB^{2}+B^{3}$
5) $ \displaystyle (A-B)^{3}=A^{3}-3A^{2}B+3AB^{2}-B^{3}$
6) $ \displaystyle A^{3}+B^{3}=(A+B)\left( {A^{2}-AB+B^{2}} \right)$
7) $ \displaystyle A^{3}-B^{3}=(A-B)\left( {A^{2}+AB+B^{2}} \right)$
Bài tập tìm giá trị nhỏ nhất của biểu thức – Toán lớp 8
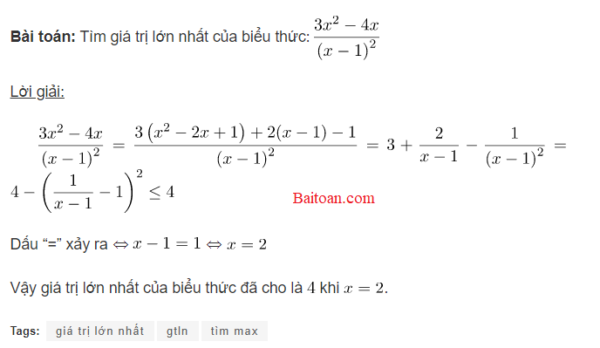
Ví dụ 1: Tìm giá trị nhỏ nhất của biểu thức: $A=x^{2}-4 x+7$
Giải
Ta có $: A=x^{2}-4 x+7=\left(x^{2}-2 \cdot 2 \cdot x+4\right)+3=(x-2)^{2}+3$
Ta luôn có : $(x-2)^{2} \geq 0$ với mọi $x$.
Suy ra: $(x-2)^{2}+3 \geq 3$ với mọi $x$.
hay $A \geq 3$ với mọi $x$.
Dấu “=” xảy ra khi : $x-2=0$ hay $x=2$
Nên : $A_{\min }=3$ khi $x=2$
Ví dụ 2: Chứng minh rằng biểu thức sau luôn dương với mọi $x$.
$B=4 x^{2}+4 x+3$
Giải
Ta có: $B=(2 x)^{2}+2 \cdot 2 x \cdot 1+1^{2}+2=(2 x+1)^{2}+2$
Ta luôn có: $(2 x+1)^{2} \geq 0$ với mọi $x$.
Suy ra: $(2 x+1)^{2}+2 \geq 2>0$ với mọi $x$.
Hay: $B>0$ với mọi $x$.
Vậy: biểu thức $B$ luôn dương với mọi $x$
Ví dụ 3: Tìm giá trị nhỏ nhất của biểu thức :
$C=x^{2}+9 y^{2}+6 x-6 y+5$
Giải
Ta có : $C=x^{2}+9 y^{2}+6 x-6 y+5$
$=\left(x^{2}+2 \cdot x \cdot 3+9\right)+\left(9 y^{2}-2 \cdot 3 y \cdot 1+1\right)-5=(x+3)^{2}+(3 y-1)^{2}-5$
Mà : $(x-2)^{2} \geq 0 ;(3 y-1)^{2} \geq 0$ với mọi $x, y$.
$(x-2)^{2}+(3 y-1)^{2} \geq 0$ với mọi $x, y$
Suy ra: $(x+3)^{2}+(3 y-1)^{2}-5 \geq-5$ với mọi $x, y$.
hay: $C \geq-5$ với mọi $x, y$
Dấu “=” xảy ra khi : $x+3=0$ và $3 y-1=0$
$x=-3 $ và $\displaystyle y=\dfrac{1}{3}$
Nên: $C_{\min }=-5$ khi $x=-3$ và $\displaystyle y=\dfrac{1}{3}$