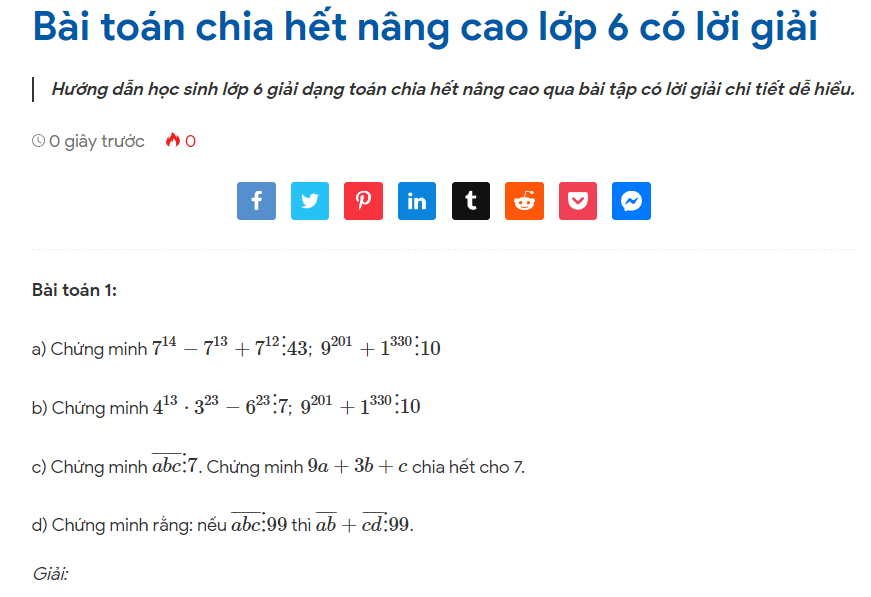
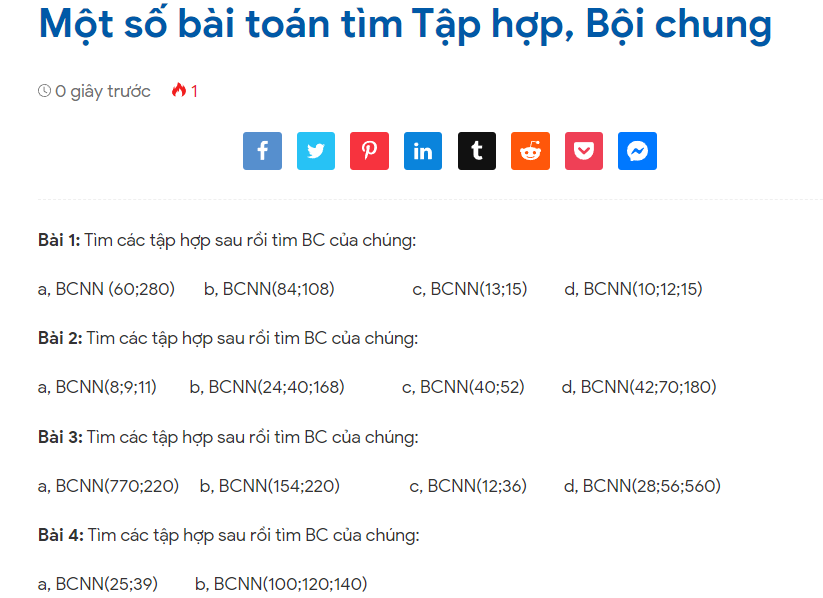
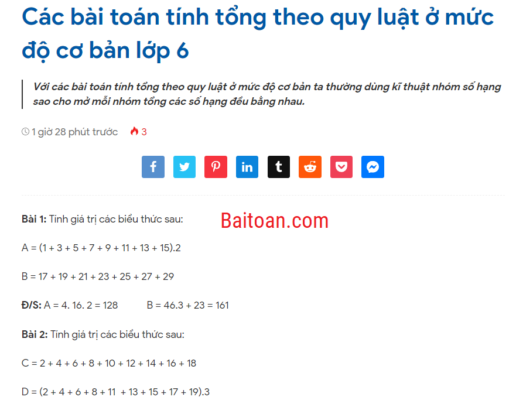
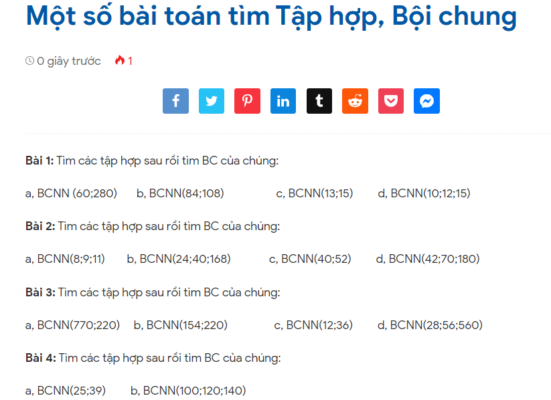
Bài toán: So sánh B với 1 biết:
$ \displaystyle B=\dfrac{1}{5}+\dfrac{1}{6}+\dfrac{1}{7}+\ldots +\dfrac{1}{{17}}$
Giải:
Ta có: $ \displaystyle \dfrac{1}{5}>\dfrac{1}{{10}};\,\,\dfrac{1}{6}>\dfrac{1}{{10}};\,\,\dfrac{1}{7}>\dfrac{1}{{10}};\,\,\dfrac{1}{8}>\dfrac{1}{{10}};\,\,\dfrac{1}{9}>\dfrac{1}{{10}}$
⇒ $ \displaystyle \dfrac{1}{5}+\dfrac{1}{6}+\dfrac{1}{7}+\,\dfrac{1}{8}+\dfrac{1}{9}>\dfrac{5}{{10}}=\dfrac{1}{2}$ (1)
$ \displaystyle \dfrac{1}{{10}}+\dfrac{1}{{11}}+\dfrac{1}{{12}}+\dfrac{1}{{13}}+\dfrac{1}{{14}}>\dfrac{5}{{15}}=\dfrac{1}{3}$ (2)
$ \displaystyle \dfrac{1}{{15}}+\dfrac{1}{{16}}+\dfrac{1}{{17}}>\dfrac{3}{{18}}=\dfrac{1}{6}$ (2)
Cộng 2 về của (1), (2) và 3 ta được:
$ \displaystyle \dfrac{1}{5}+\dfrac{1}{6}+\dfrac{1}{7}+\ldots +\dfrac{1}{{17}}>\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{6}=1$
Vậy B > 1.