Giải Toán Trung học cơ sở – lớp 6, 7, 8, 9. Các bài toán cơ bản, nâng cao, bồi dưỡng học sinh giỏi, ôn thi học kì, cuối cấp.
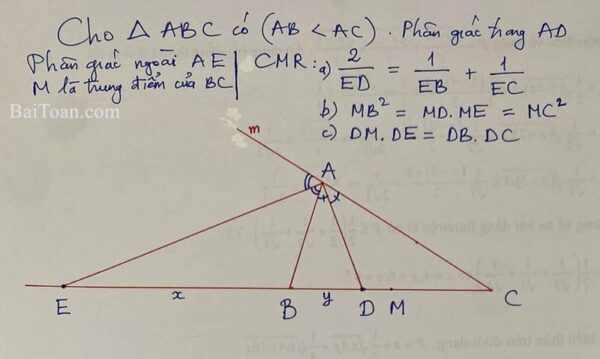
Bài toán 1: Cho tam giác ABC có trung tuyến AM, đường thẳng song song với BC cắt AB và AC lần lượt tại E và F. Chứng minh AM đi qua trung điểm của EF. Giải bằng kiến thức học kì 1 (hết chương 2) lớp 8. Không dùng định lý Talet và tam […]
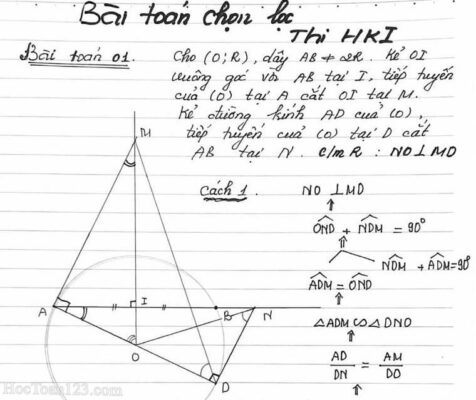
Bài toán: Cho nửa đường tròn (O;R) có AB là đường kính. Vẽ các tiếp tuyến Ax, By của nửa đường tròn (O;R). Trên nửa đường tròn (O;R) lấy điểm M (MA<MB). Tiếp tuyến tại M của nửa đường tròn (O;R) cắt Ax tại C và By tại D. a) Chứng minh: CD= AC+BD b) […]
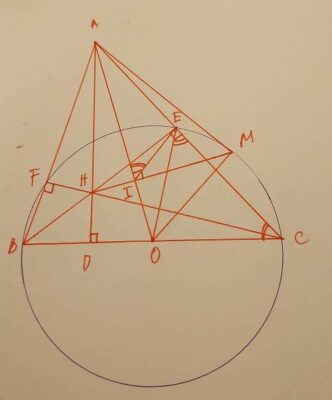
Bài toán: Cho ΔABC nhọn (AB<AC). Vẽ đường tròn (O) đường kính BC, đường tròn (O) cắt AB, AC lần lượt tại F, E. BE cắt CF tại H, AH cắt BC tại D. Vẽ HI ⊥ OA tại I. a) Chứng minh: A, E, H, F cùng thuộc đường tròn, xác định tâm S. […]
Bài toán: Tính a + b biết a, b là 2 số nguyên tố thỏa mãn a^2 – 7b – 4 = 0. Giải:
Bài toán: Chứng minh không tồn tại n nguyên để n^2 + 12n + 2022 là số chính phương. Giải:
Bài toán: Tìm 3 số nguyên tố có tích bằng 5 lần tổng của 3 số đó. Giải: Cách của Bình: để tránh xét nhiều trường hợp, có thể sử dụng thêm tính chất sắp xếp biến do tính chất đối xứng của hai biến B và c! Ko mất tính tổng quát, giả sử […]
5 cách giải cho một bài toán hình học khó phần đường tròn thi hết học kì 1 Toán lớp 9 được chia sẻ bởi cô Thanh Loan.
Bài toán: Cho tam giác ABC nhọn, các đường cao AD, BE, CF. Chứng minh cot A + cot B + cot C ≥ √3. Giải:
Bài toán: Cho $x, y \in \mathbb{Q}$ thỏa mãn $21 x^2-36 x y+44 y^2 \leq 27$. Tìm max min của $A=x+2 y$. Giải: Vì $A = x + 2y$ nên $2y = A – x$. Ta viết lại biểu thức ban đầu: $\begin{array}{c} 21{x^2} – 18x\left( {A – x} \right) + 11{\left( {A – x} […]
