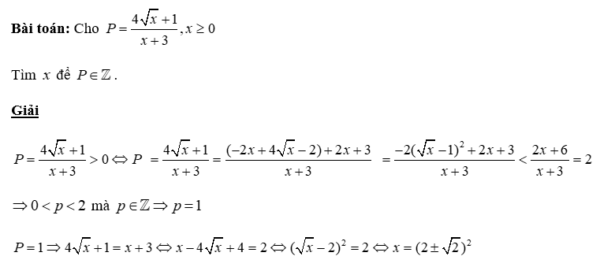Trung học cơ sở

Bài toán 1: Quãng đường đi từ A đến B dài 80 km. Một xe máy đi từ A đến B, khởi hành lúc 7 giờ. Hỏi xe máy phải đi với vận tốc ít nhất bao nhiêu km/h để đến B không quá 9 giờ cùng ngày? Giải: Để đến B không quá 9 […]

Bài toán 1:  La tông là một hợp kim của đồng và kẽm. Một khối la tông có khối lượng 10 kg chứa 80% đồng. Hỏi phải thêm vào đó bao nhiêu kẽm nguyên chất để được hợp kim la tông có chứa 70% đồng. Giải: Khối lượng đồng có trong 1 khối la tông […]

Bài toán: Cho 0 =< a; b; c =< 2 và ab + bc + ca = 4. Tìm Max, Min của P = (b+c)/(a+2) + (c+a)/(b+2) + (a+b)/(c+2) Lời giải (Phạm Văn Tuyên):

Bài toán: Một học sinh được giao thiết kế một cái hộp dạng hình hộp chữ nhật thỏa mãn: Tổng của chiều dài và chiều rộng bằng 12cm, tổng của chiều rộng và chiều cao là 24cm. Giáo viên yêu cầu học sinh ấy thiết kế sao cho thể tích cái hộp lớn nhất, giá […]

Bài toán: Tìm GTLN của $A=\dfrac{x^2}{x^4+x^2+1}$. Giải: Trường hợp x ≠ 0 chia cả tử và mẫu của phân thức cho $x^2$.

Bài toán: Cho $P=\dfrac{4\sqrt {x}+1}{x+3},x\ge 0$ Tìm $x$ để $P\in \mathbb{Z}$. Giải $\begin{aligned} P & =\dfrac{4 \sqrt{x}+1}{x+3}>0 \\ P & =\dfrac{4 \sqrt{x}+1}{x+3}=\dfrac{(-2 x+4 \sqrt{x} *-2)+2 x+3}{x+3} \\ & =\dfrac{-2(\sqrt{x}-1)^2+2 x+3}{x+3}<\dfrac{2 x+6}{x+3}=2\end{aligned}$ $\Rightarrow 0<p<2$ mà $ p\in \mathbb{Z}\Rightarrow p=1$ $P=1\Rightarrow 4\sqrt {x}+1=x+3\Leftrightarrow x-4\sqrt {x}+4=2\Leftrightarrow {(\sqrt {x}-2)^2}=2\Leftrightarrow x={(2\pm \sqrt {2})^2}$

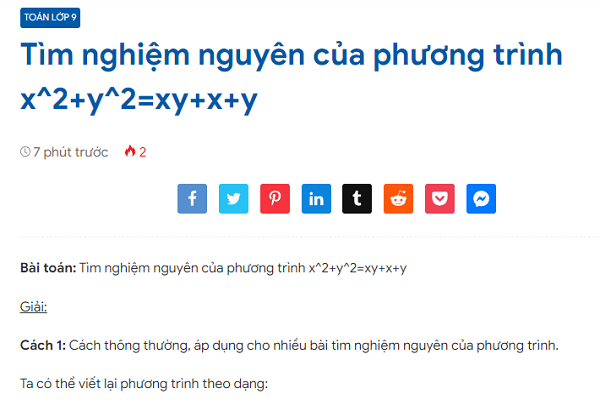
Bài toán: Tìm nghiệm nguyên của phương trình x^2+y^2=xy+x+y Giải: Cách 1: Cách thông thường, áp dụng cho nhiều bài tìm nghiệm nguyên của phương trình. Ta có thể viết lại phương trình theo dạng: x^2 – x(y+1) + y^2 – y = 0 Đây là một phương trình bậc hai đối với x, với […]

Đề bài và lời giải ở trong hình dưới đây:  

Bài toán: Giải phương trình vô tỷ $ \displaystyle y^{2}-2y-y\sqrt{{2y+3}}+6=0$ Giải: Điều kiện: $ \displaystyle {y\ge \dfrac{{-3}}{2}}$ $ \displaystyle y^{2}-2y-y\sqrt{{2y+3}}+6=0$ $ \displaystyle \Leftrightarrow 2y^{2}-4y-2y\sqrt{{2y+3}}+12=0$ $ \displaystyle \Leftrightarrow \left( {y^{2}-6y+9} \right)+\left( {y^{2}-2y\sqrt{{2y+3}}+2y+3} \right)=0$ $ \displaystyle \Leftrightarrow (y-3)^{2}+(y-\sqrt{{2y+3}})^{2}=0$ $ \displaystyle \Leftrightarrow y=3$ (thỏa mãn) Vậy $y=3$ là nghiệm của phương trình đã cho.

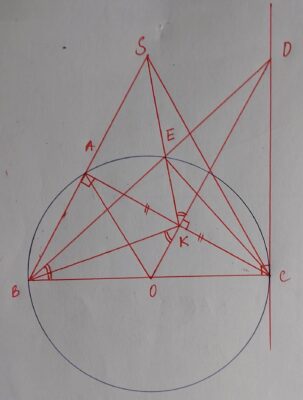
Bài toán: Cho ΔABC nội tiếp (O) có đường kính BC sao cho AB<AC. Gọi K là trung điểm của AC, tiếp tuyến tại C của (O) và tia OK cắt nhau ở D. a) Chứng minh OK ⊥ AC, b) BD cắt (O) tại E. Chứng minh DE.DB=DK.DO c) Gọi S là giao điểm […]