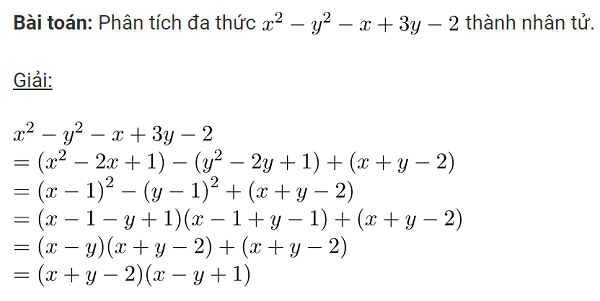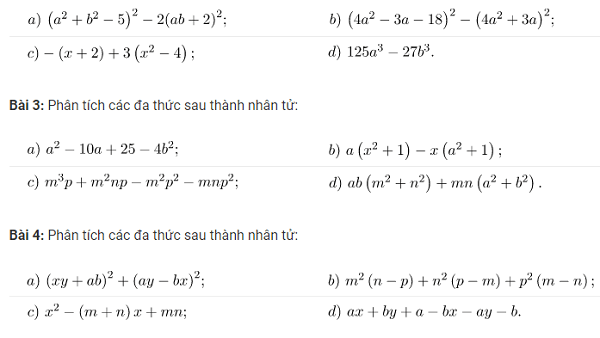Bài toán: Cho x, y, z là các số dương
Rút gọn $A=\dfrac{7 x^{3}+y^{3}+12 z^{3}}{2 x^{2} y+3 x y z+5 x z^{2}}$ biết $x^{3}+y^{3}+z^{3}=3 x y z$.
Hướng dẫn giải:
Đây là dạng toán nâng cao đòi hỏi các em phải biết áp dụng bất đẳng thức Cosi cho 3 số:
Đó là:
Với $a, b, c$ là các số thực không âm, khi đó ta có:
$\dfrac{a+b+c}{3} \geq \sqrt[3]{a b c}$
Dấu “=” xảy ra khi và chỉ khi $a = b = c$.
Áp dụng: $ \displaystyle x^{3}+y^{3}+z^{3}\ge 3xyz$
Dấu “=” xảy ra khi và chỉ khi $x = y = z$.
Từ đó thay vào ta sẽ rút gọn được biểu thức A.