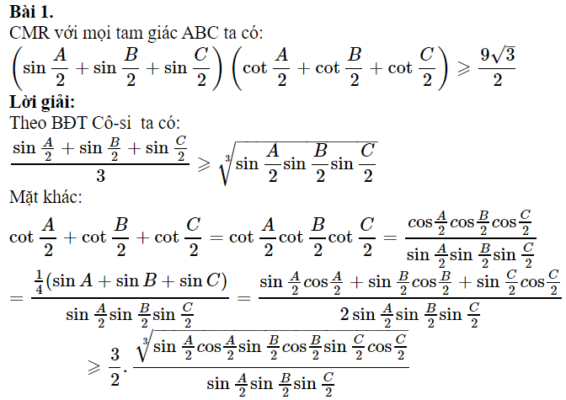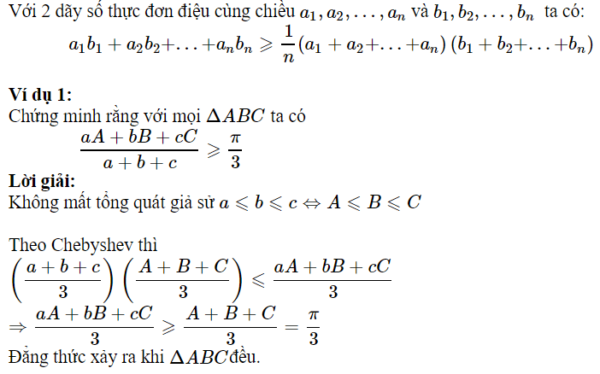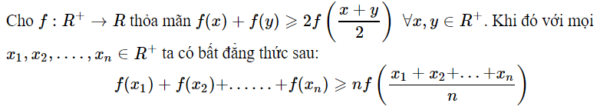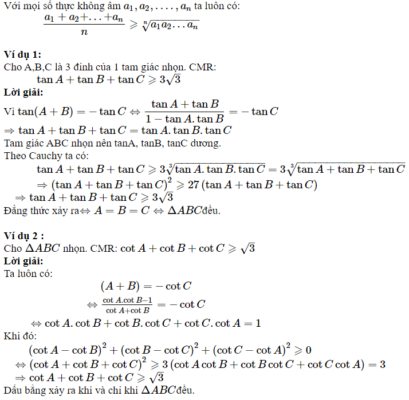Bài toán: Có bao nhiêu số có 3 chữ số mà tổng các chữ số bằng 5?Hướng dẫn giải:Tách 5 thành tổng của 3 số rồi lập số.5 = 0+0+5 -> 500;5=0+1+4 -> 410; 401; 104; 140;5=0+2+3 -> 230; 203; 302; 320;5=1+1+3-> 113; 131; 311;5=1+2+2 -> 122; 212; 221.Vậy có 15 số.
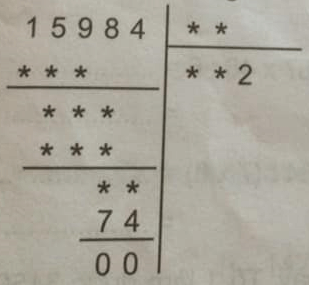
Bài toán: Thay dấu sao bằng chữ số thích hợp rồi viết lại phép chia.Hướng dẫn giải:Dựa vào số 74 khi nhân ngược lên kia để tìm số chia.2 x ** = 74=> ** = 74:2= 37Từ đó có phép chia là: 15984:37Điền số hợp lý khi thực hiện chia bình thường
Bài toán: Tìm hai số chẵn có tổng bằng 2416 biết giữa chúng có 3 số chẵn khác nhau.Thực chất là bài toán tìm 2 số khi biết tổng và hiệu của 2 số. Hiệu của hai số chưa nói cụ thể và cần phải tính.Lời giải:Giữa 2 số có 3 số chẵn khác nhau […]
Problem: Natalia, who is always in a hurry, went up the escalator by making one step every second. This way it took her 20 steps to get upstairs. The next day she made 2 steps every second on her way up, and this time it took her 32 steps to get upstairs. How many steps […]
Bằng cách áp dụng các bất đẳng thức đã học chúng ta có thể áp dụng vào bài toán chứng minh BĐT lượng giác có lời giải dưới đây.
Bất đẳng thức Chebyshev cũng được sử dụng để chứng minh BĐT lượng giác trong chương trình toán THPT.
Bất đẳng thức Jensen thật sự là một công cụ chuyên dùng cho chứng minh các bất đẳng thức lượng giác. Tuy không phải là một bất đẳng thức chặt nhưng nếu thấy có những dấu hiệu của BĐT Jensen, chúng ta nên dùng ngay.
Bất đẳng thức Bunhiacốpxki cùng với BĐT Cauchy (Cô si) được sử dụng nhiều để chứng minh BĐT lượng giác. Mời các bạn xem ví dụ dưới đây.
Bất đẳng thức Cauchy (AM-GM hay Cô si) được sử dụng rất rộng rãi trong các bài toán chứng minh BĐT lượng giác. Cùng tham khảo các ví dụ dưới đây.Chú ý là BĐT Cosi chỉ áp dụng với số thực không âm.
Nhận biết về số lượng: Một – Nhiều – Bằng nhau là những bài toán mà cha mẹ, thầy cô cần phải dạy cho các bé ngay từ khi còn học lớp mầm non.