Giải bài toán tìm giá trị lớn nhất lớp 8
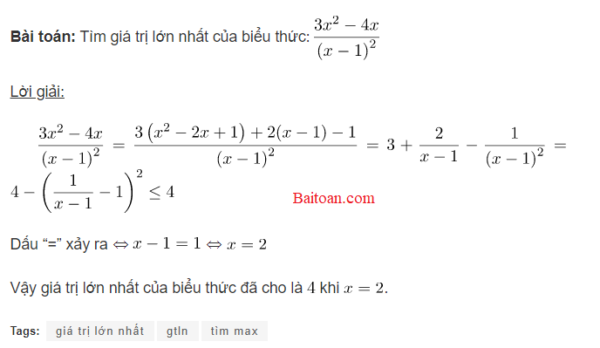
Bài toán: Tìm giá trị lớn nhất của biểu thức: $ \displaystyle \frac{{3{{x}^{2}}-4x}}{{{{{(x-1)}}^{2}}}}$ Lời giải: $ \displaystyle \frac{{3{{x}^{2}}-4x}}{{{{{(x-1)}}^{2}}}}=\frac{{3\left( {{{x}^{2}}-2x+1} \right)+2(x-1)-1}}{{{{{(x-1)}}^{2}}}}=3+\frac{2}{{x-1}}-\frac{1}{{{{{(x-1)}}^{2}}}}=4-{{\left( {\frac{1}{{x-1}}-1} \right)}^{2}}\le 4$ Dấu “=” xảy ra ⇔ $x – 1 = 1$ ⇔ $x = 2$ Vậy giá trị lớn nhất của biểu thức đã cho là $4$ khi $x = 2$.